
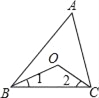
【题目】(1)如图,在△ABC中,∠ABC和∠ACB的平分线相交于点O,若∠A=42°,求∠BOC的度数;
(2)把(1)中∠A=42°这个条件去掉,试探索∠BOC和∠A之间有怎样的数量关系.
【答案】(1)111°(2)证明见解析
【解析】试题分析:(1)根据角平分线的定义得到∠1=![]() ∠ABC,∠2=
∠ABC,∠2=![]() ∠ACB,再根据三角形内角和定理得到∠1+∠2+∠COB=180°,∠ABC+∠ACB+∠A=180°,经过变形后得到∠BOC=90°+
∠ACB,再根据三角形内角和定理得到∠1+∠2+∠COB=180°,∠ABC+∠ACB+∠A=180°,经过变形后得到∠BOC=90°+![]() ∠A,然后把∠A=40°代入计算即可;
∠A,然后把∠A=40°代入计算即可;
(2)利用上面的证明方法,直接可证明∠BOC=90°+![]() ∠A.
∠A.
试题解析:(1)∵∠A=42°,
∴∠ABC+∠ACB=180°﹣∠A=138°,
∵BO、CO分别是△ABC的角∠ABC、∠ACB的平分线,
∴∠1=![]() ∠ABC,∠2=
∠ABC,∠2=![]() ∠ACB,
∠ACB,
∴∠1+∠2=![]() (∠ABC+∠ACB)=
(∠ABC+∠ACB)=![]() ×138°=69°,
×138°=69°,
∴∠BOC=180°﹣(∠1+∠2)=180°﹣69°=111°;
(2)∵BO、CO分别是△ABC的角∠ABC、∠ACB的平分线,
∴∠1=![]() ∠ABC,∠2=
∠ABC,∠2=![]() ∠ACB,
∠ACB,
∴∠1+∠2=![]() (∠ABC+∠ACB)=
(∠ABC+∠ACB)=![]() (180°﹣∠A),
(180°﹣∠A),
∴∠BOC=180°﹣(∠1+∠2)=180°﹣![]() (180°﹣∠A)=90°+
(180°﹣∠A)=90°+![]() ∠A.
∠A.


科目:初中数学 来源: 题型:
【题目】如图,边长为6的大正方形中有两个小正方形,若两个小正方形的面积分别为S1、S2 , 则S1+S2的值为( )

A. 16 B. 17 C. 18 D. 19
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】运用等式性质进行的变形,不正确的是( )
A.如果a=b,那么a﹣c=b﹣c
B.如果a=b,那么a+c=b+c
C.如果a=b,那么ac=bc
D.如果ac=bc,那么a=b
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】衢州市“十二五”规划纲要指出,力争到2015年,全市农民人均年纯收入超13000元,数13000用科学记数法可以表示为( )
A.13×103
B.1.3×104
C.0.13×104
D.130×102
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,已知AB=BC=CA=4cm,AD⊥BC于D,点P、Q分别从B、C两点同时出发,其中点P沿BC向终点C运动,速度为1cm/s;点Q沿CA、AB向终点B运动,速度为2cm/s,设它们运动的时间为x(s).
(1)求x为何值时,PQ⊥AC;
(2)设△PQD的面积为![]() ,当0<x<2时,求y与x的函数关系式;
,当0<x<2时,求y与x的函数关系式;
(3)当0<x<2时,求证:AD平分△PQD的面积;
(4)探索以PQ为直径的圆与AC的位置关系,请写出相应位置关系的x的取值范围(不要求写出过程).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=ax2+bx+c(a≠0)的大致图象如图,关于该二次函数,下列说法错误的是( )

A. 函数有最小值
B. 对称轴是直线x=![]()
C. 当x<![]() ,y随x的增大而减小
,y随x的增大而减小
D. 当﹣1<x<2时,y>0
查看答案和解析>>
科目:初中数学 来源: 题型:
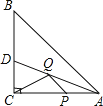
【题目】如图,在△ABC中,∠C=90°,CB=CA=4,∠A的平分线交BC于点D,若点P、Q分别是AC和AD上的动点,则CQ+PQ的最小值是___________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com