
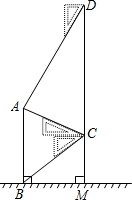
 如图,某中学在教学楼前新建了一座雕塑AB.为了测量雕塑的高度,小明在二楼找到一点C,利用三角尺测得雕塑顶端点A的仰角为30°,底部点B的俯角为45°,小华在五楼找到一点D,利用三角尺测得点A的俯角为60°.若CD为9.6m,则雕塑AB的高度为多少?(结果精确到0.1m,参考数据:$\sqrt{3}$≈1.73).
如图,某中学在教学楼前新建了一座雕塑AB.为了测量雕塑的高度,小明在二楼找到一点C,利用三角尺测得雕塑顶端点A的仰角为30°,底部点B的俯角为45°,小华在五楼找到一点D,利用三角尺测得点A的俯角为60°.若CD为9.6m,则雕塑AB的高度为多少?(结果精确到0.1m,参考数据:$\sqrt{3}$≈1.73). 分析 首先过点C作CE⊥AB于E,然后利用三角函数的性质,求得CD,AC的长,然后在Rt△ACE中,求得AE的长,继而求得CE的长,又在Rt△BCE中,求得BE的长,继而求得答案.
解答 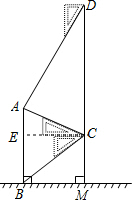 解:过点C作CE⊥AB于E.
解:过点C作CE⊥AB于E.
∵∠ADC=90°-60°=30°,∠ACD=90°-30°=60°,
∴∠CAD=90°.
∵CD=9.6,
∴AC=$\frac{1}{2}$CD=4.8.
在Rt△ACE中,∵∠AEC=90°,∠ACE=30°,
∴AE=$\frac{1}{2}$AC=2.4,
CE=AC•cos∠ACE=4.8•cos30°=$\frac{12\sqrt{3}}{5}$.
在Rt△BCE中,∵∠BCE=45°,
∴BE=CE=$\frac{12\sqrt{3}}{5}$,
∴AB=AE+BE=2.4+$\frac{12\sqrt{3}}{5}$≈6.6(米).
答:雕塑AB的高度约为6.6米.
点评 本题考查了解直角三角形的应用-仰角俯角问题,要求学生借助俯角构造直角三角形,并结合图形利用三角函数解直角三角形.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:填空题
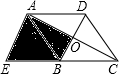 如图,在菱形ABCD中,对角线AC和BD的长分别为8和6,将BD沿CB方向平移,使D和A重合,B和CB延长线上的E点重合,则阴影部分的面积为18.
如图,在菱形ABCD中,对角线AC和BD的长分别为8和6,将BD沿CB方向平移,使D和A重合,B和CB延长线上的E点重合,则阴影部分的面积为18.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
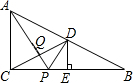 如图,在Rt△ABC中,∠ACB=90°,点D是AB边的中点,过D作DE⊥BC于点E,点P是边BC上的一个动点,AP与CD相交于点Q.当AP+PD的值最小时,AQ与PQ之间的数量关系是( )
如图,在Rt△ABC中,∠ACB=90°,点D是AB边的中点,过D作DE⊥BC于点E,点P是边BC上的一个动点,AP与CD相交于点Q.当AP+PD的值最小时,AQ与PQ之间的数量关系是( )| A. | AQ=$\frac{5}{2}$PQ | B. | AQ=3PQ | C. | AQ=$\frac{8}{3}$PQ | D. | AQ=4PQ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,四边形ABCD中,对角线相交于点O,E、F、G、H分别是AD、BD、BC、AC的中点,要使四边形EFGH是菱形,则四边形ABCD需满足的条件是( )
如图,四边形ABCD中,对角线相交于点O,E、F、G、H分别是AD、BD、BC、AC的中点,要使四边形EFGH是菱形,则四边形ABCD需满足的条件是( )| A. | AB=AD | B. | AC=BD | C. | AD=BC | D. | AB=CD |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
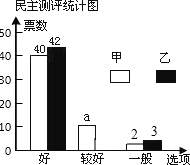 九年级一班邀请A、B、C、D、E五位评委对甲、乙两位同学的才艺表演打分,并组织全班50名同学对两人民意测评投费,绘制了如下的统计表和不完整的条形统计图:
九年级一班邀请A、B、C、D、E五位评委对甲、乙两位同学的才艺表演打分,并组织全班50名同学对两人民意测评投费,绘制了如下的统计表和不完整的条形统计图:| A | B | C | D | E | |
| 甲 | 89 | 91 | 93 | 94 | 86 |
| 乙 | 88 | 87 | 90 | 98 | 92 |

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
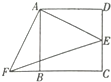 如图,四边形ABCD是正方形,F分别是DC和BC的延长线上的点,且DE=BF,连结AE,AF,EF.
如图,四边形ABCD是正方形,F分别是DC和BC的延长线上的点,且DE=BF,连结AE,AF,EF.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com