
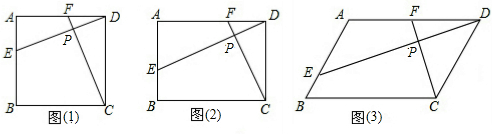
分析 (2)根据∠A=∠ADC=90°,DE⊥CF,证明∠ADE=∠DCF,得到△ADE∽△DCF,得到答案;
(3)在AD的延长线上取点M,使CM=CF,证明△ADE∽△DCM,得到答案.
解答 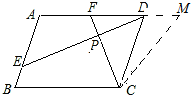 (2)证明:∵四边形ABCD是矩形,
(2)证明:∵四边形ABCD是矩形,
∴∠A=∠ADC=90°,又∵DE⊥CF,
∴∠ADE=∠DCF,
∴△ADE∽△DCF,
∴$\frac{DE}{CF}$=$\frac{AD}{CD}$;
(3)当∠B+∠EPC=180°时,$\frac{DE}{CF}$=$\frac{AD}{CD}$成立.
证明:在AD的延长线上取点M,使CM=CF,
则∠CMF=∠CFM,
∵AD∥BC,
∴∠CFM=∠FCB,
∵AB∥CD,
∴∠A=∠CDM,又∵∠B+∠EPC=180°,
∴∠AED=∠FCB,
∴∠CMF=∠AED,
∴△ADE∽△DCM,
∴$\frac{DE}{CM}$=$\frac{AD}{CD}$,即$\frac{DE}{CF}$=$\frac{AD}{CD}$.
点评 本题考查的是正方形、矩形和平行四边形的性质,灵活运用三角形全等和相似的判定和性质、正确作出辅助线是解题的关键.


科目:初中数学 来源: 题型:选择题
 如图是由几个相同的小正方体搭建的几何体的俯视图,小正方形中的数字表示在该位置的小正方体的个数,这个几何体的主视图是( )
如图是由几个相同的小正方体搭建的几何体的俯视图,小正方形中的数字表示在该位置的小正方体的个数,这个几何体的主视图是( )| A. |  | B. |  | C. |  | D. |  |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,直线l1∥l2,且分别于△ABC的两边AB相交.若∠A=50°,∠1=35°,则∠2的度数为( )
如图,直线l1∥l2,且分别于△ABC的两边AB相交.若∠A=50°,∠1=35°,则∠2的度数为( )| A. | 35° | B. | 65° | C. | 85° | D. | 95° |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com