
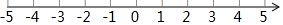 在数轴上表示下列各数,并把这些数按从小到大顺序进行排列,用“<”连接:-1.5,-22,-(-4),0,-|-3|,$\sqrt{9}$.
在数轴上表示下列各数,并把这些数按从小到大顺序进行排列,用“<”连接:-1.5,-22,-(-4),0,-|-3|,$\sqrt{9}$. 科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
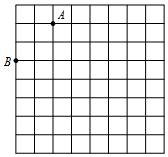 如图是规格为8×8的正方形网格(小正方形的边长为1,小正方形的顶点叫格点),所给网格中按下列要求操作:
如图是规格为8×8的正方形网格(小正方形的边长为1,小正方形的顶点叫格点),所给网格中按下列要求操作:查看答案和解析>>
科目:初中数学 来源: 题型:填空题
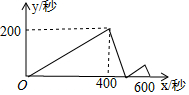 甲、乙两人在同一直线道路上同起点、同方向、同时出发,分别以不同的速度匀速跑步1500米,当甲超出乙200米时,甲停下来等候乙,甲、乙会合后,两人分别以原来的速度继续跑向终点,先到终点的人在终点休息,在跑步的整个过程中,甲、乙两人的距离y(米)与乙出发的时间x(秒)之间的关系如图所示,则甲到终点时,乙跑了1450 米.
甲、乙两人在同一直线道路上同起点、同方向、同时出发,分别以不同的速度匀速跑步1500米,当甲超出乙200米时,甲停下来等候乙,甲、乙会合后,两人分别以原来的速度继续跑向终点,先到终点的人在终点休息,在跑步的整个过程中,甲、乙两人的距离y(米)与乙出发的时间x(秒)之间的关系如图所示,则甲到终点时,乙跑了1450 米.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
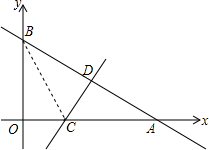 如图,一次函数y=-$\frac{3}{4}$x+6的图象与x轴和y轴分别交于点A和B,再将△AOB沿直线CD对折,使点A与点B重合.直线CD与x轴交于点C,与AB交于点D.
如图,一次函数y=-$\frac{3}{4}$x+6的图象与x轴和y轴分别交于点A和B,再将△AOB沿直线CD对折,使点A与点B重合.直线CD与x轴交于点C,与AB交于点D.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
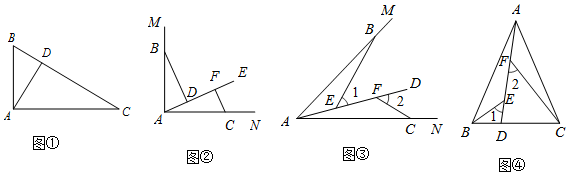
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
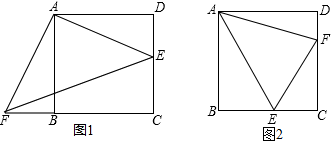
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com