
【题目】如图,已知在![]() 中,AD是
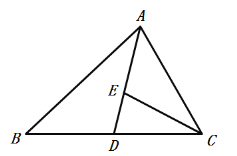
中,AD是![]() 的中线,∠DAC=∠B,点E在边AD上,CE=CD.
的中线,∠DAC=∠B,点E在边AD上,CE=CD.
(1)求证:![]() ;
;
(2)求证:![]() .
.
【答案】(1)见解析;(2)见解析.
【解析】
(1)由CE=CD=BD转化比例式,再证出△ACE∽△BAD即可;
(2)由(1)中相似可得出,DC2=ADAE①,再证△ACD∽△BCA,得出AC2=BC·CD=2CD2②,结合①②即可得出结果.
证明:(1)∵AD为△ABC的中线,
∴BD=CD,
∵CD=CE,
∴BD=CD=CE,
∴∠CDE=∠CED,
∵∠CDE=∠B+∠BAD,∠CED=∠DAC+∠ACE,∠DAC=∠B,
∴∠BAD=∠ACE
∵△ACE∽△BAD,
∴![]()
∴![]() ;
;
(2)∵△ACE∽△BAD,
∴![]() ,
,
∴BDCE=AEAD,
∴DC2=ADAE①.
∵∠DAC=∠B,∠ACD=∠ACB,
∴△ACD∽△BCA,
∴![]()
∴AC2=BC·CD=2CD2②,
∴由①②可得,![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】我省南部的南宫山景区,为吸引游客组团来此旅游特推出了如下门票收费标准:
标准一:如果人数不超过20人,门票价格70元/人
标准二:如果人数超过20人,每超过1人,门票价格降低2元,但门票价格不低于55元/人
(1)若某单位组织22名员工去南宫山景区旅游,则购买门票共需多少元?
(2)若某单位共支付南宫山景区门票费用1500元,试求该单位这次共有多少名员工去南宫山旅游.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,一枚质地均匀的正六面体骰子的六个面分别标有数字![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,如图2,正方形
,如图2,正方形![]() 的顶点处各有一个圈,跳圈游戏的规则为:游戏者每掷一次骰子,骰子朝上的那面上的数字是几,就沿正方形的边按顺时针方向连续跳几个边长。如:若从圈
的顶点处各有一个圈,跳圈游戏的规则为:游戏者每掷一次骰子,骰子朝上的那面上的数字是几,就沿正方形的边按顺时针方向连续跳几个边长。如:若从圈![]() 起跳,第一次掷得
起跳,第一次掷得![]() ,就顺时针连续跳
,就顺时针连续跳![]() 个边长,落在圈
个边长,落在圈![]() ;若第二次掷得
;若第二次掷得![]() ,就从圈
,就从圈![]() 开始顺时针连续跳
开始顺时针连续跳![]() 个边长,落得圈
个边长,落得圈![]() ;…设游戏者从圈
;…设游戏者从圈![]() 起跳.
起跳.

(1)小贤随机掷一次骰子,求落回到圈![]() 的概率
的概率![]() .
.
(2)小南随机掷两次骰子,用列表法求最后落回到圈![]() 的概率
的概率![]() ,并指出他与小贤落回到圈
,并指出他与小贤落回到圈![]() 的可能性一样吗?
的可能性一样吗?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某服装店在服装销售中发现:进货价每件60元,销售价每件100元的某服装每天可售出20件,为了迎接新春佳节,服装店决定采取适当的促销措施,扩大销售量,增加盈利.经调查发现:如果每件服装降价1元,那么每天就可多售出2件.
(1)如果服装店想每天销售这种服装盈利1050元,同时又要使顾客得到更多的实惠,那么每件服装应降价多少元?
(2)每件服装降价多少元时,服装店每天可获得最大利润?最大利润是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在Rt![]() 中,∠A=90°,AC=4,
中,∠A=90°,AC=4,![]() ,将
,将![]() 沿着斜边BC翻折,点A落在点
沿着斜边BC翻折,点A落在点![]() 处,点D、E分别为边AC、BC的中点,联结DE并延长交
处,点D、E分别为边AC、BC的中点,联结DE并延长交![]() 所在直线于点F,联结
所在直线于点F,联结![]() ,如果
,如果![]() 为直角三角形时,那么
为直角三角形时,那么![]() ____________
____________
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图在△ABC中,∠C=90°,点O在AC上,以AO为半径的⊙O交AB于D, BD的垂直平分线交BD于F,交BC于E,连接DE.
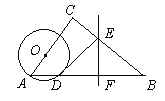
(1)求证:DE是⊙O的切线;
(2)若∠B=30°,BC=![]() ,且AD∶DF=1∶2,求⊙O的直径.
,且AD∶DF=1∶2,求⊙O的直径.
查看答案和解析>>
科目:初中数学 来源: 题型:
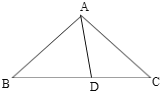
【题目】如图,在等腰△ABC中,AB=AC=4,BC=6点D在底边BC上,且∠DAC=∠ACD,将△ACD沿着AD所在直线翻折,使得点C落到点E处,联结BE,那么BE的长为______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】等腰△ABC的直角边AB=BC=10cm,点P、Q分别从A、C两点同时出发,均以1cm/秒的相同速度作直线运动,已知P沿射线AB运动,Q沿边BC的延长线运动,PQ与直线AC相交于点D.设P点运动时间为t,△PCQ的面积为S.
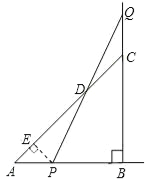
(1)求出S关于t的函数关系式;
(2)当点P运动几秒时,S△PCQ=S△ABC?
(3)作PE⊥AC于点E,当点P、Q运动时,线段DE的长度是否改变?证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,我们定义直线y=ax-a为抛物线y=ax2+bx+c(a、b、c为常数,a≠0)的“衍生直线”;有一个顶点在抛物线上,另有一个顶点在y轴上的三角形为其“衍生三角形”.已知抛物线![]() 与其“衍生直线”交于A、B两点(点A在点B的左侧),与x轴负半轴交于点C.
与其“衍生直线”交于A、B两点(点A在点B的左侧),与x轴负半轴交于点C.
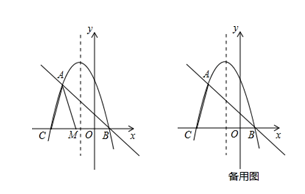
(1)填空:该抛物线的“衍生直线”的解析式为 ,点A的坐标为 ,点B的坐标为 ;
(2)如图,点M为线段CB上一动点,将△ACM以AM所在直线为对称轴翻折,点C的对称点为N,若△AMN为该抛物线的“衍生三角形”,求点N的坐标;
(3)当点E在抛物线的对称轴上运动时,在该抛物线的“衍生直线”上,是否存在点F,使得以点A、C、E、F为顶点的四边形为平行四边形?若存在,请直接写出点E、F的坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com