
【题目】如图1,在![]() 中,
中,![]() 是角平分线,
是角平分线,![]() 是
是![]() 上的点,
上的点, ![]() 相交于点
相交于点![]() .
.
(1) 如图2,若![]() =90°,求证:
=90°,求证: ![]()
![]() ;
;
(2) 如图1,若![]() =
=![]() ( 0°<
( 0°< ![]() <180°).
<180°).
①求![]()
![]() 的值(用含
的值(用含![]() 的代数式表示);
的代数式表示);
②是否存在![]() ,使
,使![]() 小于
小于![]() ,如果存在,求出
,如果存在,求出![]() 的范围,如果不存在,请说明理由.
的范围,如果不存在,请说明理由.

 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,将矩形AOCD沿直线AE折叠(点E在边DC上),折叠后端点D恰好落在边OC上的点F处.若点D的坐标为(10,8),则点E的坐标为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线 ![]() 与
与 ![]() 轴、
轴、 ![]() 轴分别相交于点A(-1,0)和B(0,3),其顶点为D.
轴分别相交于点A(-1,0)和B(0,3),其顶点为D.
(1)求这条抛物线的解析式;
(2)若抛物线与 ![]() 轴的另一个交点为E,求△ODE的面积;抛物线的对称轴上是否存在点P使得△PAB的周长最短.若存在请求出点P的坐标,若不存在说明理由.
轴的另一个交点为E,求△ODE的面积;抛物线的对称轴上是否存在点P使得△PAB的周长最短.若存在请求出点P的坐标,若不存在说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,E是AB上一点,F是AD延长线上一点,且DF=BE.

(1)求证:CE=CF;
(2)若点G在AD上,且∠GCE=45°,则GE=BE+GD成立吗?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将边长为6的正三角形纸片ABC按如下顺序进行两次折叠,展平后,得折痕AD,BE(如图①),点O为其交点.
(1)探求AO到OD的数量关系,并说明理由;
(2)如图②,若P,N分别为BE,BC上的动点.
(Ⅰ)当PN+PD的长度取得最小值时,求BP的长度;
(Ⅱ)如图③,若点Q在线段BO上,BQ=1,则QN+NP+PD的最小值= ![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明的妈妈在菜市场买回3斤萝卜、2斤排骨,准备做萝卜排骨汤.
妈妈:“今天买这两样菜共花了45元,上月买同重量的这两样菜只要36元”;
爸爸:“报纸上说了萝卜的单价上涨50%,排骨单价上涨20%”;
小明:“爸爸、妈妈,我想知道今天买的萝卜和排骨的单价分别是多少?”
请你通过列方程(组)求解这天萝卜、排骨的单价(单位:元/斤).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠1=∠2,CF⊥AB,DE⊥AB,求证:FG∥BC.
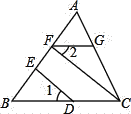
证明:∵CF⊥AB,DE⊥AB (______)
∴∠BED=90°,∠BFC=90° (______)
∴∠BED=∠BFC (______)
∴ED∥FC (______)
∴∠1=∠BCF (______)
∵∠1=∠2 (______)
∴∠2=∠BCF (______)
∴FG∥BC (______)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将一副三角尺(在Rt△ABC中,∠ACB=90°,∠B=60°;在Rt△DEF中,∠EDF=90°,∠E=45°)如图①摆放,点D为AB的中点,DE交AC于点P,DF经过点C.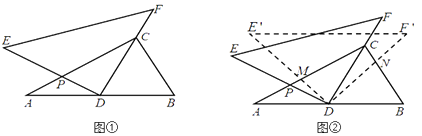
(1)求∠ADE的度数;
(2)如图②,将△DEF绕点D顺时针方向旋转角 ![]() ,此时等腰直角三角尺记为
,此时等腰直角三角尺记为 ![]() ,
, ![]() 交AC于点M,
交AC于点M, ![]() 交BC于点N,试判断
交BC于点N,试判断 ![]() 的值是否随着
的值是否随着 ![]() 的变化而变化?如果不变,请求出
的变化而变化?如果不变,请求出 ![]() 的值;反之,请说明理由.
的值;反之,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com