
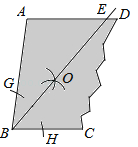
【题目】如图,一块余料ABCD,AD∥BC,现进行如下操作:以点B为圆心,适当长为半径画弧,分别交BA,BC于点G,H;再分别以点G,H为圆心,大于![]() GH的长为半径画弧,两弧在∠ABC内部相交于点O,画射线BO,交AD于点E.
GH的长为半径画弧,两弧在∠ABC内部相交于点O,画射线BO,交AD于点E.
(1)求证:AB=AE;
(2)若∠A=100°,求∠EBC的度数.
 中考解读考点精练系列答案
中考解读考点精练系列答案科目:初中数学 来源: 题型:
【题目】“丹棱冻粑”是眉山著名特色小吃,产品畅销省内外,现有一个产品销售点在经销时发现:如果每箱产品盈利10元,每天可售出50箱;若每箱产品涨价1元,日销售量将减少2箱.
(1)现该销售点每天盈利600元,同时又要顾客得到实惠,那么每箱产品应涨价多少元?
(2)若该销售点单纯从经济角度考虑,每箱产品应涨价多少元才能获利最高?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,点O为直线AB上一点,过点O作射线OC,使∠BOC=120°.将一直角三角板的直角顶点放在点O处,一边OM在射线OB上,另一边ON在直线AB的下方.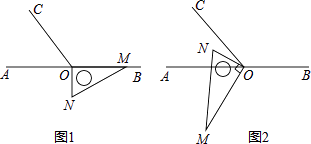
(1)将图1中的三角板绕点O按每秒10°的速度沿逆时针方向旋转一周.在旋转的过程中,假如第t秒时,OA、OC、ON三条射线构成相等的角,求此时t的值为多少?
(2)将图1中的三角板绕点O顺时针旋转图2,使ON在∠AOC的内部,请探究:∠AOM与∠NOC之间的数量关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某兴趣小组决定去市场购买A,B,C三种仪器,其单价分别为3元,5元,7元,购买这批仪器需花62元;经过讨价还价,最后以每种单价各下降1元成交,结果只花50元就买下了这批仪器.那么A种仪器最多可买( )
A.8件 B.7件 C.6件 D.5件
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】情境观察: 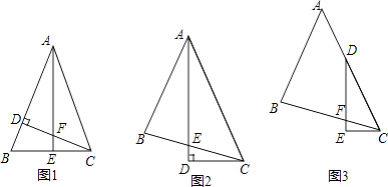
(1)如图1,△ABC中,AB=AC,∠BAC=45°,CD⊥AB,AE⊥BC,垂足分别为D、E,CD与AE交于点F. ①写出图1中所有的全等三角形;
②线段AF与线段CE的数量关系是 .
(2)如图2,△ABC中,∠BAC=45°,AB=BC,AD平分∠BAC,AD⊥CD,垂足为D,AD与BC交于点E. 求证:AE=2CD.
(3)如图3,△ABC中,∠BAC=45°,AB=BC,点D在AC上,∠EDC= ![]() ∠BAC,DE⊥CE,垂足为E,DE与BC交于点F.求证:DF=2CE. 要求:请你写出辅助线的作法,并在图3中画出辅助线,不需要证明.
∠BAC,DE⊥CE,垂足为E,DE与BC交于点F.求证:DF=2CE. 要求:请你写出辅助线的作法,并在图3中画出辅助线,不需要证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,过∠AOB平分线上一点C作CD∥OB交OA于点D,E是线段OC的中点,请过点E画直线分别交射线CD、OB于点M、N,探究线段OD、ON、DM之间的数量关系,并证明你的结论.
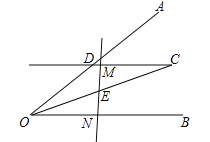
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市将大、中、小学生的视力进行抽样分析,其中大、中、小学生的人数比为2:3:5,若已知中学生被抽到的人数为150人,则应抽取的样本容量等于( )
(A)1500 (B)1000 (C)150 (D)500
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com