
【题目】(本小题满分8分)
如图,用两段等长的铁丝恰好可以分别围成一个正五边形和一个正六边形,其中正五边形的边长为(![]() )
)![]() ,正六边形的边长为(
,正六边形的边长为(![]() )cm(其中
)cm(其中![]() ),求这两段铁丝的总长
),求这两段铁丝的总长

【答案】解:由已知得.正五边形周长为![]() ,正六边形周长为
,正六边形周长为![]() .
.
因为正五边形和正六边形的周长相等.所以![]()
整理得,![]() ,配方得
,配方得![]() .解得
.解得![]() ,
,![]() (舍去)
(舍去)
故正五边形的周长为![]()
又因为两段铁丝等长,所以这两段铁丝的总长为420cm.
答:这两段铁丝的总长为420cm.
【解析】
试题根据正五边形和正六边形的周长相等,列一元二次方程求x的值,得出正六边形的边长,再根据所求边长即可求两段铁丝的总长.
试题解析:由已知得,正五边形周长为5(x2+17)cm,正六边形周长为6(x2+2x)cm,
∵正五边形和正六边形的周长相等,
∴5(x2+17)=6(x2+2x),
整理得x2+12x-85=0,配方得(x+6)2=121,
解得x1=5,x2=-17(舍去),
故正五边形的周长为![]() (cm).
(cm).
又因为两段铁丝等长,所以这两段铁丝的总长为420cm.
答:这两段铁丝的总长为420cm.
考点: 一元二次方程的应用.


科目:初中数学 来源: 题型:
【题目】根据几何图形的面积关系可以形象直观地表示多项式的乘法,例如(a+b)(p+q)=ap+aq+bp+bq可以用图(1)表示:


(1)根据图(2),写出一个多项式乘以多项式的等式.
(2)从A、B两题中任选一题作答.
A.请画一个几何图形,表示(x+p)(x+q)=x2+(p+q)x+pq,并仿照上图标明相应的字母.
B. 请画一个几何图形,表示(x-p)(x-q)=x2-(p+q)x+pq,并仿照上图标明相应的字母.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图锐角△ABC,若∠ABC=40°,∠ACB=70°,点D、E在边AB、AC上,CD与BE交于点H.
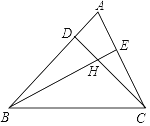
(1)若BE⊥AC,CD⊥AB,求∠BHC的度数.
(2)若BE、CD平分∠ABC和∠ACB,求∠BHC的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】越来越多的人在用微信付款、转账.把微信账户里的钱转到银行卡叫做提现,自2016年3月1日起,每个微信账户终身享有1000元的免费提现额度,当累计提现金额超过1000元时,超出的部分需支付0.1%的手续费,以后每次提现支付的手续费均为提现金额的0.1%,
(1)小明用自己的微信账户第一次提现金额为1500元,需支付手续费 元.
(2)小丽使用微信至今,用自己的微信账户共提现三次,提现金额和手续费如下:
第一次 | 第二次 | 第三次 | |
提现金额 | a | b | 2a+3b |
手续费/元 | 0 | 0.2 | 3.1 |
求小丽前两次提现的金额分别为多少元.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们知道“两边和一角分别相等的两个三角形不一定全等”,如图(1),![]() ,
,![]() ,
,![]() ,但
,但![]() 与
与![]() 却不全等.但是如果两个直角三角形呢?如图(2)
却不全等.但是如果两个直角三角形呢?如图(2)![]() ,
,![]() ,
,![]() ,则
,则![]() 吗?
吗?

(1)根据图(2)完成以下证明和阅读:
![]() 和
和![]() 中,
中,![]()
![]() ,
,![]() ____________(勾股定理)
____________(勾股定理)
![]() ,
,![]() ____________
____________
![]() ,
,![]() .
.![]() ____________
____________
在![]() 与
与![]() 中,
中,![]() ,
,![]() ,
,![]()
![]() ____________(____________)
____________(____________)
归纳:斜边和一条直角边相等的两个直角三角形全等;简称为“斜边直角边”或“![]() ”.
”.
几何语言如下:
在![]() 与
与![]() 中,
中,![]()
![]() ,
,![]()
![]()
(2)如图(3)已知![]() ,
,![]() ;求证:
;求证:![]() 平分
平分![]() .(每一步都要填写理由)
.(每一步都要填写理由)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一只渔船在灯塔C的正西方向10海里的A处,以20海里/时的速度沿北偏东30°方向行驶.
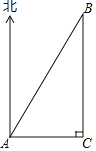
(1)多长时间后,渔船距灯塔最近?
(2)多长时间后,渔船行驶到灯塔的正北方向?此时渔船距灯塔有多远?(其中:202-102=17.32)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我市开展“美丽泰安,创卫同行”活动,某校倡议学生利用双休日在某公园参加义务劳动,为了解同学们劳动情况,学校随机调查了部分同学的劳动时间,并用得到的数据绘制了不完整的统计图,根据图中信息可知扇形图中的“1.5小时”部分圆心角的度数是________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,把6张长为a、宽为b(a>b)的小长方形纸片不重叠地放在长方形ABCD内,未被覆盖的部分(两个长方形)用阴影表示,设这两个长方形的面积的差为S.当BC的长度变化时,按照同样的放置方式,S始终保持不变,则a、b满足( )

A. a=1.5bB. a=2.5bC. a=3bD. a=2b
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com