
【题目】已知:如图,在菱形ABCD中,E是AB上一点,线段DE与菱形对角线AC交于点F,点O是AC的中点,EO的延长线交边DC于点G
(1)求证:∠AED=∠FBC;
(2)求证:四边形DEBG是平行四边形.
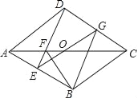
【答案】(1)见解析;(2)见解析.
【解析】
(1)首先证明△CBF≌△CDF,从而得到∠FBC=∠FDC,然后由平行线的性质可知∠FDC=∠AED,从而可证得∠AED=∠FBC;
(2)连接BD,由菱形的性质可知;OB=OD,然后再证明OG=OE,从而可证得四边形DEBG是平行四边形.
(1)∵四边形ABCD是菱形,
∴∠DCF=∠BCF,DC=BC.
在△DCF和△BCF中,
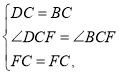
∴△DCF≌△BCF,
∴∠FBC=∠FDC.
∵DC∥AB,
∴∠FDC=∠AED.
∴∠AED=∠FBC.
(2)如图,连接BD.
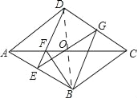
∵四边形ABCD是菱形,O是AC的中点,
∴OD=OB.
∵DC∥AB,
∴∠GCO=∠EAO.
在△GCO和△EAO中,
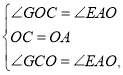
∴△GCO≌△EAO,
∴OE=OG.
∴四边形DEBG是平行四边形.


 优百分课时互动系列答案
优百分课时互动系列答案科目:初中数学 来源: 题型:
【题目】水果店张阿姨以每斤2元的价格购进某种水果若干斤,然后以每斤4元的价格出售,每天可售出100斤.通过调查发现,这种水果每斤的售价每降低0.1元,每天可多售出20斤.为保证每天至少售出260斤,张阿姨决定降价销售.
(1)若将这种水果每斤的售价降低![]() 元,则每天的销售量是__________斤(用含
元,则每天的销售量是__________斤(用含![]() 的代数式表示);
的代数式表示);
(2)销售这种水果要想每天盈利300元,张阿姨需将每斤的售价降低多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了响应“倡导绿色出行、从身边做起”,小李将上班方式由自驾车改为骑共享单车,他从家到达上班地点,自驾车要走的路程为8.4千米,骑共享单车要走的路程为6千米,已知小李自驾车的速度是骑共享单车速度的2.4倍,他由自驾车改为骑共享单车后,时间多用了10分钟.求小李自驾车和骑共享单车的速度分别是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
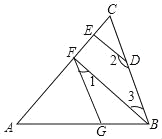
【题目】如图,DE⊥AC于点E,BF⊥AC于点F,∠1+∠2=180°,求证:∠AGF=∠ABC.
试将下面的证明过程补充完整(填空):
证明:∵DE⊥AC,BF⊥AC(已知)
∴∠AFB=∠AED=90°(_______)
∴BF∥DE(同位角相等,两直线平行),
∴∠2+∠3=180°(两直线平行,同旁内角互补),
又∵∠1+∠2=180°(已知),
∴∠1=______,(同角的补角相等)
∴GF∥_____(内错角相等,两直线平行),
∴∠AGF=∠ABC.(______)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一节数学课上,老师布置了一个任务:
已知,如图1,在![]() 中,
中,![]() ,用尺规作图作矩形
,用尺规作图作矩形![]() .
.
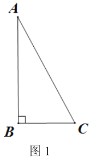
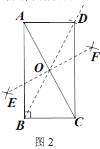
同学们开动脑筋,想出了很多办法,其中小亮作了图2,他向同学们分享了作法:
①分别以点![]() 、
、![]() 为圆心,大于
为圆心,大于![]() 长为半径画弧,两弧分别交于点
长为半径画弧,两弧分别交于点![]() 、
、![]() ,连接
,连接![]() 交
交![]() 于点
于点![]() ;
;
②作射线![]() ,在
,在![]() 上取点
上取点![]() ,使
,使![]() ;
;
③连接![]() ,
,![]() .
.
则四边形![]() 就是所求作的矩形.
就是所求作的矩形.
老师说:“小亮的作法正确.”
写出小亮的作图依据.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司到果品基地购买某种优质水果慰问医务工作者,果品基地对购买量在3000kg以上(含3000kg)的顾客采用两种销售方案,甲方案:每千克9元,由基地送货上门;乙方案:每千克8元,由自己租车运回,已知该公司租车从基地到公司的运输费用为5000元
(1)分别写出该公司两种购买方案付款金额![]() (元)与所购的水果
(元)与所购的水果![]() 之间的函数关系式,并写出自变量
之间的函数关系式,并写出自变量![]() 的取值范围.
的取值范围.
(2)依据购买量判断,选择哪种方案付款少?并说理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
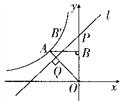
【题目】如图,反比例函数![]() (k<0)的图象经过点A(-1,1),过点A作AB⊥y轴,垂足为B,在y轴的正半轴上取一点P(0,t),过点P作直线OA的垂线l,以直线l为对称轴,点B经轴对称变换得到了点B’在此反比例函数的图象上,则t的值是( )
(k<0)的图象经过点A(-1,1),过点A作AB⊥y轴,垂足为B,在y轴的正半轴上取一点P(0,t),过点P作直线OA的垂线l,以直线l为对称轴,点B经轴对称变换得到了点B’在此反比例函数的图象上,则t的值是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“2018东台西溪半程马拉松”的赛事共有两项:A、“半程马拉松”、 B、“欢乐跑”。小明参加了该项赛事的志愿者服务工作, 组委会随机将志愿者分配到两个项目组.
(1)小明被分配到“半程马拉松”项目组的概率为________.
(2)为估算本次赛事参加“半程马拉松”的人数,小明对部分参赛选手作如下调查:
调查总人数 | 20 | 50 | 100 | 200 | 500 |
参加“半程马拉松”人数 | 15 | 33 | 72 | 139 | 356 |
参加“半程马拉松”频率 | 0.750 | 0.660 | 0.720 | 0.695 | 0.712 |
①请估算本次赛事参加“半程马拉松”人数的概率为_______.(精确到0.1)
②若本次参赛选手大约有3000人,请你估计参加“半程马拉松”的人数是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com