
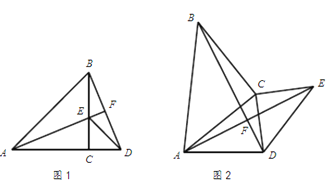
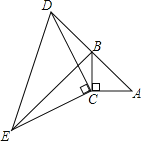
【题目】在△ABC和△DEC中,AC=BC,DC=EC,∠ACB=∠ECD=90°.
(1)如图1,当点A、C、D在同一条直线上时,AC=12,EC=5,
①求证:AF⊥BD; ②求AF的长度;
(2)如图2,当点A、C、D不在同一条直线上时,求证:AF⊥BD.
【答案】(1)①证明见解析;②![]() ;(2)证明见解析.
;(2)证明见解析.
【解析】试题分析:(1)①证明△ACE≌△BCD,得到∠1=∠2,由对顶角相等得到∠3=∠4,所以∠BFE=∠ACE=90°,即可得结论;②根据勾股定理求出BD,利用△ABD的面积的两种表示方法,即可解答;(2)证明△ACE≌△BCD,得到∠1=∠2,又由∠3=∠4,得到∠BFA=∠BCA=90°,即可得结论.
试题解析:
(1)①证明:如图1,

∵在△ACE和△BCD中,

∴△ACE≌△BCD,
∴∠1=∠2,
∵∠3=∠4,
∴∠BFE=∠ACE=90°,
∴AF⊥BD.
②∵∠ECD=90°,BC=AC=12,DC=EC=5,
∴根据勾股定理得:BD=13,
∵S△ABD=![]() ADBC=
ADBC=![]() BDAF,
BDAF,
即![]()
∴AF=![]() .
.
(2)证明:如图2,

∵∠ACB=∠ECD,
∴∠ACB+∠ACD=∠ECD+∠ACD,
∴∠BCD=∠ACE,
在△ACE≌△BCD中
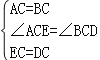
∴△ACE≌△BCD(SAS),
∴∠1=∠2,
∵∠3=∠4,
∴∠BFA=∠BCA=90°,
∴AF⊥BD.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】请把下面证明过程补充完整:
已知:如图,∠ADC=∠ABC,BE、DF分别平行∠ABC、∠ADC,且∠1=∠2.
求证:∠A=∠C.
证明:因为BE、DF分别平分∠ABC、∠ADC,( ).
所以∠1=![]() ∠ABC,∠3=
∠ABC,∠3=![]() ∠ADC( ).
∠ADC( ).
因为∠ABC=∠ADC(已知),
所以∠1=∠3( ),
因为∠1=∠2(已知),
所以∠2=∠3( ).
所以 ∥ ( ).
所以∠A+∠ =180°,∠C+∠ =180°( ).
所以∠A=∠C( ).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,E为AC上一点,且AE=BC,过点A作AD⊥CA,垂足为A,且AD=AC,AB、DE交于点F.试判断线段AB与DE的数量关系和位置关系,并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】推理填空:
如图,已知∠1=∠2,∠B=∠C,可推得AB∥CD.理由如下:
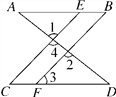
∵∠1=∠2(已知),且∠1=∠4(____________),
∴∠2=∠4(等量代换),
∴CE∥BF(__________________________),
∴∠________=∠3(______________________).
又∵∠B=∠C(已知),
∴∠3=∠B(等量代换).
∴AB∥CD(__________________________).
查看答案和解析>>
科目:初中数学 来源: 题型:
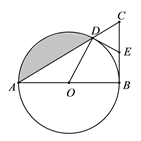
【题目】如图,△ABC中,∠ABC=90°,以AB为直径的⊙O交AB于点D,点E为BC的中点,连接OD、DE.
⑴ 求证:OD⊥DE.
⑵ 若∠BAC=30°,AB=8,求阴影部分的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,池塘边有块长为20m,宽为10m的长方形土地,现在将其余三面留出宽都是xm的小路,中间余下的长方形部分做菜地,用含x的式子表示:
(1)菜地的长a= m,菜地的宽b= m;菜地的周长C= m;
(2)求当x=1m时,菜地的周长C.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ACB=90°,AC=BC,延长AB至点D,使DB=AB,连接CD,以CD为直角边作等腰直角三角形CDE,其中∠DCE=90°,连接BE.
(1)求证:△ACD≌△BCE;
(2)若AC=3,求BE的长度.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com