
 如图,直线y=-$\frac{\sqrt{3}}{3}$x+3和x轴、y轴的交点分别为B,C,点A的坐标是(-$\sqrt{3}$,0),∠ABC=30°,若动点M从B点出发沿BC运动,运动的速度为每秒1个单位长度,当点M运动到C点时停止运动,设点M运动t秒时,△ABM的面积为S.
如图,直线y=-$\frac{\sqrt{3}}{3}$x+3和x轴、y轴的交点分别为B,C,点A的坐标是(-$\sqrt{3}$,0),∠ABC=30°,若动点M从B点出发沿BC运动,运动的速度为每秒1个单位长度,当点M运动到C点时停止运动,设点M运动t秒时,△ABM的面积为S.分析 (1)首先作MN⊥AB于点N,连接AM,分别求出BM、MN的长度各是多少;然后根据直线y=-$\frac{\sqrt{3}}{3}$x+3和x轴、y轴的交点分别为B,C,求出点B、C的坐标各是多少,进而求出AB的长度是多少;最后根据三角形的面积公式,求出S与t的函数关系式即可.
(2)首先根据三角形的面积的求法,求出△ABC的面积是多少;然后根据S=$\frac{1}{2}{S}_{△ABC}$,求出t的值是多少即可.
(3)根据题意,分三种情况:①点P在x轴上时;②点P在y轴上,且BP为斜边时;③点P在y轴上,且BP为另一条直角边时;然后根据直角三角形的性质分类讨论,求出P点坐标各是多少即可.
解答 解:(1)如图1,作MN⊥AB于点N,连接AM,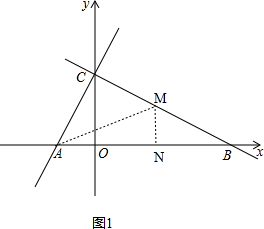 ,
,
∵点M运动的速度为每秒1个单位长度,
∴点M运动t秒时,BM=t,
∵∠ABC=30°,∠MNB=90°,
∴MN=$\frac{1}{2}$BM=$\frac{1}{2}$t,
∵直线y=-$\frac{\sqrt{3}}{3}$x+3和x轴、y轴的交点分别为B,C,
∴B(3$\sqrt{3}$,0),C(0,3),
又∵点A的坐标是(-$\sqrt{3}$,0),
∴AB=3$\sqrt{3}$-(-$\sqrt{3}$)=4$\sqrt{3}$,
∴S=$\frac{1}{2}$×4$\sqrt{3}$×$\frac{1}{2}$t=$\sqrt{3}$t.
(2)∵AB=4$\sqrt{3}$,OC=3,
∴S△ABC=$\frac{1}{2}×4\sqrt{3}×3$=6$\sqrt{3}$,
由$\sqrt{3}$t=$\frac{1}{2}$×6$\sqrt{3}$=3$\sqrt{3}$,
解得t=3,
∴当t为3时,S=$\frac{1}{2}{S}_{△ABC}$.
(3)当t=4时,在坐标轴上存在点P,使得△BMP是以BM为直角边的直角三角形.
①如图2,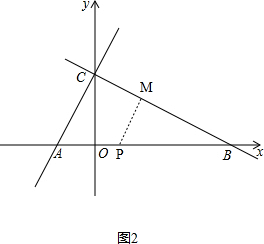 ,
,
∵点M运动的速度为每秒1个单位长度,
∴当t=4时,BM=4,
∵∠ABC=30°,∠PMB=90°,
∴BP=BM÷cos30°=4÷$\frac{\sqrt{3}}{2}$=$\frac{8}{3}\sqrt{3}$,
∴OP=OB-BP=3$\sqrt{3}$-$\frac{8}{3}\sqrt{3}$=$\frac{\sqrt{3}}{3}$,
∴点P的坐标是($\frac{\sqrt{3}}{3}$,0).
②如图3,PM和AB相交于点N,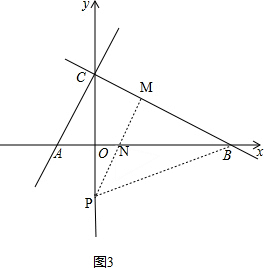 ,
,
∵点M运动的速度为每秒1个单位长度,
∴当t=4时,BM=4,
∵∠ABC=30°,∠NMB=90°,
∴BN=BM÷cos30°=4÷$\frac{\sqrt{3}}{2}$=$\frac{8}{3}\sqrt{3}$,
∴ON=OB-BN=3$\sqrt{3}$-$\frac{8}{3}\sqrt{3}$=$\frac{\sqrt{3}}{3}$,
∵∠MNB=90°-30°=60°,∠ONP=∠MNB,
∴∠ONP=60°,
∴OP=ON•tan60°=$\frac{\sqrt{3}}{3}×\sqrt{3}=1$,
∴点P的坐标是(0,-1).
③如图4,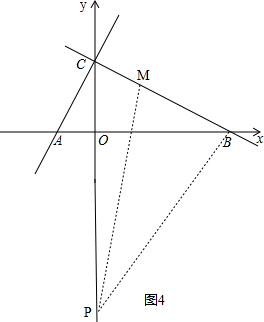 ,
,
∵OC=3,∠ABC=30°,∠BOC=90°,
∴BC=2×3=6,∠PCB=90°-30°=60°,
又∵∠PBC=90°,
∴∠BPC=90°-60°=30°,
∴CP=2BC=2×6=12,
∴OP=CP-OC=12-3=9,
∴点P的坐标是(0,-9).
综上,可得
当t=4时,在坐标轴上存在点P,使得△BMP是以BM为直角边的直角三角形,
点P的坐标是($\frac{\sqrt{3}}{3}$,0)、(0,-1)或(0,-9).
点评 (1)此题主要考查了一次函数综合题,考查了分析推理能力,考查了分类讨论思想的应用,考查了数形结合思想的应用,考查了从已知函数图象中获取信息,并能利用获取的信息解答相应的问题的能力.
(2)此题还考查了行程问题中速度、时间和路程的关系:速度×时间=路程,路程÷时间=速度,路程÷速度=时间,要熟练掌握.
(3)此题还考查了直角三角形的性质和应用,以及三角形的面积的求法,要熟练掌握.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题

| A. | 0个 | B. | 1个 | C. | 2个 | D. | 3个 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
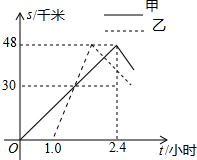 四川芦山“4•20”7.0级地震发生后,各方力量向灾区源源不断的运送救援人力、物资,并发起爱心捐款、捐物.一方有难八方支援,举国上下无不心系雅安.某单位组织一批救援物质紧急送往灾区,甲、乙两车分别从A地将一批救援物质运往芦山县大川镇,再返回A地,如图表示两车离A地的距离s(千米)随时间t(小时)变化的图象,已知乙车到达B地后以30千米/小时的速度返回.请根据图象中的信息,当甲车从A地返回的速度为48km/h时,才能与乙车同时回到A地.
四川芦山“4•20”7.0级地震发生后,各方力量向灾区源源不断的运送救援人力、物资,并发起爱心捐款、捐物.一方有难八方支援,举国上下无不心系雅安.某单位组织一批救援物质紧急送往灾区,甲、乙两车分别从A地将一批救援物质运往芦山县大川镇,再返回A地,如图表示两车离A地的距离s(千米)随时间t(小时)变化的图象,已知乙车到达B地后以30千米/小时的速度返回.请根据图象中的信息,当甲车从A地返回的速度为48km/h时,才能与乙车同时回到A地.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
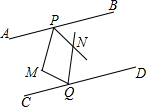 如图,M为两条平行线AB、CD之间的一点,P、Q分别在直线AB、CD上,∠BPM、∠DQM的平分线交于点N,若∠M=100°,则∠PNQ的度数为( )
如图,M为两条平行线AB、CD之间的一点,P、Q分别在直线AB、CD上,∠BPM、∠DQM的平分线交于点N,若∠M=100°,则∠PNQ的度数为( )| A. | 100° | B. | 110° | C. | 120° | D. | 130° |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,一段抛物线:y=-x(x-3)(0≤x≤3),记为C1,它与x轴交于点O,A1;将C1绕点A1旋转180°得C2,交x轴于点A2;将C2绕点A2旋转180°得C3,交x轴于点A3;…如此进行下去,直至得C17.若P(50,m)在第17段抛物线C17上,则m=2.
如图,一段抛物线:y=-x(x-3)(0≤x≤3),记为C1,它与x轴交于点O,A1;将C1绕点A1旋转180°得C2,交x轴于点A2;将C2绕点A2旋转180°得C3,交x轴于点A3;…如此进行下去,直至得C17.若P(50,m)在第17段抛物线C17上,则m=2.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com