
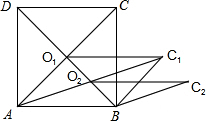
 如图,正方形ABCD的面积为2$\sqrt{5}$cm2,对角线交于点O1,以AB、AO1为邻边做平行四边形AO1C1B,对角线交于点O2,以AB、AO2为邻边做平行四边形AO2C2B,…,以此类推,则平行四边形AO6C6B的面积为$\frac{\sqrt{5}}{{2}^{5}}$cm2.
如图,正方形ABCD的面积为2$\sqrt{5}$cm2,对角线交于点O1,以AB、AO1为邻边做平行四边形AO1C1B,对角线交于点O2,以AB、AO2为邻边做平行四边形AO2C2B,…,以此类推,则平行四边形AO6C6B的面积为$\frac{\sqrt{5}}{{2}^{5}}$cm2. 分析 设平行四边形ABC1O1的面积为S1,推出S△ABO1=$\frac{1}{2}$S1,又S△ABO1=$\frac{1}{4}$S正方形,推出S1=$\frac{1}{2}$S正方形;设ABC2O2为平行四边形为S2,由S△ABO2=$\frac{1}{2}$S2,又S△ABO2=$\frac{1}{8}$S正方形,推出S2=$\frac{1}{4}$S正方形,观察探究规律后即可解决问题.
解答 解:∵设平行四边形ABC1O1的面积为S1,
∴S△ABO1=$\frac{1}{2}$S1,
又∵S△ABO1=$\frac{1}{4}$S正方形,
∴S1=$\frac{1}{2}$S正方形,
设ABC2O2为平行四边形为S2,
∴S△ABO2=$\frac{1}{2}$S2,
又∵S△ABO2=$\frac{1}{8}$S正方形,
∴S2=$\frac{1}{4}$S正方形,
…,
同理:设ABC6O6为平行四边形为S6,S6=$\frac{1}{{2}^{6}}$•S正方形=$\frac{1}{{2}^{6}}$×2$\sqrt{5}$=$\frac{\sqrt{5}}{{2}^{5}}$.
故答案为$\frac{\sqrt{5}}{{2}^{5}}$.
点评 此题考查了矩形及平行四边形的性质,要求学生审清题意,找出面积之间的关系,归纳总结出一般性的结论.考查了学生观察、猜想、验证及归纳总结的能力.


科目:初中数学 来源: 题型:解答题
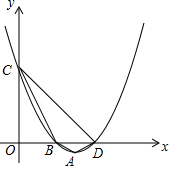 已知二次函数y=x2-(a-1)x+a-2,其中a是常数.
已知二次函数y=x2-(a-1)x+a-2,其中a是常数.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,在矩形ABCD中,AB=4,AD=6,点E是边BC的中点,连结AE,若将△ABE沿AE翻折,点B落在点F处,连结FC,则CF=( )
如图,在矩形ABCD中,AB=4,AD=6,点E是边BC的中点,连结AE,若将△ABE沿AE翻折,点B落在点F处,连结FC,则CF=( )| A. | $\frac{18}{5}$ | B. | $\frac{16}{5}$ | C. | $\frac{12}{5}$ | D. | $\frac{4}{5}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 解不等式组$\left\{\begin{array}{l}{2(x+1)≥0,①}\\{1-\frac{x}{3}>\frac{x-3}{6},②}\end{array}\right.$并把解集在数轴上表示出来.
解不等式组$\left\{\begin{array}{l}{2(x+1)≥0,①}\\{1-\frac{x}{3}>\frac{x-3}{6},②}\end{array}\right.$并把解集在数轴上表示出来.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在△ABC中,∠A=60°,点D是BC边的中点,DE⊥BC,∠ABC的角平分线BF交DE于△ABC内一点P,连接PC.
如图,在△ABC中,∠A=60°,点D是BC边的中点,DE⊥BC,∠ABC的角平分线BF交DE于△ABC内一点P,连接PC.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| x(元) | 180 | 210 | 260 | 300 |
| y(间) | 100 | 85 | 60 | 40 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com