
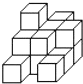
 如图所示的几何体是由16个棱长为1厘米的小正方体堆积而成的,问这个几何体的表面积是多少平方厘米?
如图所示的几何体是由16个棱长为1厘米的小正方体堆积而成的,问这个几何体的表面积是多少平方厘米?  举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案科目:初中数学 来源: 题型:填空题
 如图,某部门计划在火车站A和大学城B之间修一条长为4公里的公路,经测量在火车站A北偏东60度方向,B西偏北45度方向C处有一圆形公园,要想计划修筑的公路不会穿过公园,则公园半径最大为2($\sqrt{3}$-1)公里.
如图,某部门计划在火车站A和大学城B之间修一条长为4公里的公路,经测量在火车站A北偏东60度方向,B西偏北45度方向C处有一圆形公园,要想计划修筑的公路不会穿过公园,则公园半径最大为2($\sqrt{3}$-1)公里.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
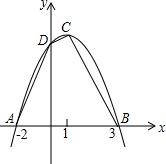 已知:如图,二次函数的图象与x轴交于A(-2,0),B(4,0)两点,且函数的最大值为9.
已知:如图,二次函数的图象与x轴交于A(-2,0),B(4,0)两点,且函数的最大值为9.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知:抛物线C1:y=x2-2x-3.
已知:抛物线C1:y=x2-2x-3.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com