
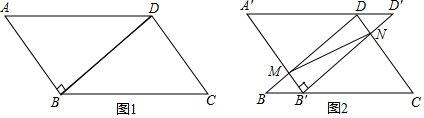
分析 (1)结论:四边形A′B′CD是平行四边形;根据两组对边分别平行的四边形是平行四边形即可判断;
(2)根据y=A′B′•DM计算即可;
(3)由MN∥BC,可得BM:DB=CN:CD,求出CN,可得方程:t:4=$\frac{3}{4}$(4-t):3,解方程即可;
解答 解:(1)结论:四边形A′B′CD是平行四边形;
理由:∵A′B′∥CD,BC′∥DA′,
∴四边形A′B′CD是平行四边形.
(2)如图2中,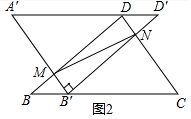
在Rt△BCD中,∵BC=5,CD=3,
∴BD=$\sqrt{{5}^{2}-{3}^{2}}$=4,
∴y=A′B′•DM=3(4-t)=-3t+12.
(3)∵MB′∥CD,
∴DM:DB=CB′:CB,
∴(4-t):4=CB′:5,
∴CB′=$\frac{5}{4}$(4-t),
∵NB′∥BD,
∴CB′:CB=CN:CD,
∴$\frac{5}{4}$(4-t):5=CN:3,
∴CN=$\frac{3}{4}$(4-t),
∵MN∥BC,
∴BM:DB=CN+CD,
∴t:4=$\frac{3}{4}$(4-t):3,
∴t=2,
∴t=2s时,MN∥BC.
点评 本题考查四边形综合题、平行四边形的性质、平行线分线段成比例定理等知识,解题的关键是灵活运用所学知识解决问题,学会利用参数解决问题,属于中考压轴题.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
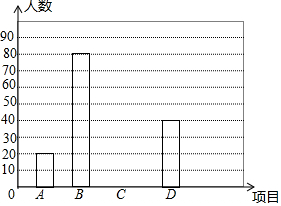 尚志市某中学为了了解学生的课余生活情况,学校决定围绕“A:欣赏音乐、B:体育运动、C:读课外书、D:其他活动中,你最喜欢的课余生活种类是什么?(只写一类)“的问题,在全校范围内随机抽取部分学生进行问卷调查,并将调查问卷适当整理后绘制成如图所示的不完整的条形统计图,其中喜欢欣赏音乐的学生占被抽取学生的10%,请你根据以上信息解答下列问题:
尚志市某中学为了了解学生的课余生活情况,学校决定围绕“A:欣赏音乐、B:体育运动、C:读课外书、D:其他活动中,你最喜欢的课余生活种类是什么?(只写一类)“的问题,在全校范围内随机抽取部分学生进行问卷调查,并将调查问卷适当整理后绘制成如图所示的不完整的条形统计图,其中喜欢欣赏音乐的学生占被抽取学生的10%,请你根据以上信息解答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,把△ABC向上平移4个单位长度,再向右平移3个单位长度,得到△A′B′C′.
如图,把△ABC向上平移4个单位长度,再向右平移3个单位长度,得到△A′B′C′.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com