Question

如图①，正方形ABCD中，点A、B的坐标分别为(0，10)，(8，4)，点C在第一象限．动点P在正方形ABCD的边上，从点A出发沿A→B→C→D匀速运动，同时动点Q以相同速度在x轴上运动，当P点到D点时，两点同时停止运动，设运动的时间为t秒．

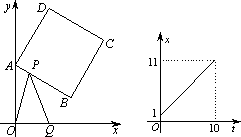
(1)当P点在边AB上运动时，点Q的横坐标x(长度单位)关于运动时间t(秒)的函数图象如图②所示，请写出点Q开始运动时的坐标及点P运动速度；

(2)求正方形边长及顶点C的坐标；

(3)在(1)中当t为何值时，△OPQ的面积最大，并求此时P点的坐标．

(4)如果点P、Q保持原速度速度不变，当点P沿A→B→C→D匀速运动时，OP与PQ能否相等，若能，写出所有符合条件的t的值；若不能，请说明理由．

Answer 1

答案：
解析：

解：(1)(1，0)　　1分 　　点P运动速度每秒钟1个单位长度．　　3分 　　(2)过点作BF⊥y轴于点，⊥轴于点，则＝8， 　　∴ 　在Rt△AFB中，　　5分 　　过点作⊥轴于点，与的延长线交于点． 　　∵　∴△ABF≌△BCH． 　　∴． 　　∴． 　　∴所求C点的坐标为(14，12)　　7分 　　(3)过点P作PM⊥y轴于点M，PN⊥轴于点N， 　　则△APM∽△ABF． 　　∴　． 　　∴　∴． 　　设△OPQ的面积为(平方单位) 　　∴(0≤≤10)　　10分 　　说明：未注明自变量的取值范围不扣分． 　　∵＜0　∴当时，△OPQ的面积最大　　11分 　　此时P的坐标为(，)　　12分 　　(4)当或时，OP与PQ相等　　14分 　　对一个加1分，不需写求解过程