
”¾ĢāÄæ”æČēĶ¼¢ŁĖłŹ¾£¬ŌŚÖ±½ĒĢŻŠĪABCDÖŠ£¬”ĻBAD=90”ć£¬EŹĒÖ±ĻßABÉĻŅ»µć£¬¹żE×÷Ö±Ļßl”ĪBC£¬½»Ö±ĻßCDÓŚµćF£®½«Ö±ĻßlĻņÓŅĘ½ŅĘ£¬ÉčĘ½ŅĘ¾ąĄėBEĪŖt£Øt”Ż0£©£¬Ö±½ĒĢŻŠĪABCD±»Ö±ĻßlÉعżµÄĆ껿£ØĶ¼ÖŠŅõÓ°²æ·Ö£©ĪŖS£¬S¹ŲÓŚtµÄŗÆŹżĶ¼ĻóČēĶ¼¢ŚĖłŹ¾£¬OMĪŖĻ߶Ī£¬MNĪŖÅ×ĪļĻßµÄŅ»²æ·Ö£¬NQĪŖÉäĻߣ¬Nµćŗį×ų±źĪŖ4£®
ŠÅĻ¢¶ĮČ”
£Ø1£©ĢŻŠĪÉĻµ×µÄ³¤AB=£»
£Ø2£©Ö±½ĒĢŻŠĪABCDµÄĆ껿=£»
Ķ¼ĻóĄķ½ā
£Ø3£©Š“³öĶ¼¢ŚÖŠÉäĻßNQ±ķŹ¾µÄŹµ¼ŹŅāŅ壻
£Ø4£©µ±2£¼t£¼4Ź±£¬ĒóS¹ŲÓŚtµÄŗÆŹż¹ŲĻµŹ½£»
ĪŹĢā½ā¾ö
£Ø5£©µ±tĪŖŗĪÖµŹ±£¬Ö±Ļßl½«Ö±½ĒĢŻŠĪABCD·Ö³ÉµÄĮ½²æ·ÖĆ껿֮±ČĪŖ1£ŗ3£®
”¾“š°ø”æ
£Ø1£©2
£Ø2£©12
£Ø3£©
½ā£ŗµ±Ę½ŅĘ¾ąĄėBE“óÓŚµČÓŚ4Ź±£¬Ö±½ĒĢŻŠĪABCD±»Ö±ĻßlÉعżµÄĆ껿ŗćĪŖ12
£Ø4£©
½ā£ŗµ±2£¼t£¼4Ź±£¬ČēĶ¼ĖłŹ¾£¬
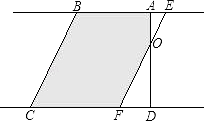
Ö±½ĒĢŻŠĪABCD±»Ö±ĻßlÉعżµÄĆ껿S=SÖ±½ĒĢŻŠĪABCD©SRt”÷DOF
=12© ![]() £Ø4©t£©”Į2£Ø4©t£©=©t2+8t©4
£Ø4©t£©”Į2£Ø4©t£©=©t2+8t©4
£Ø5£©
½ā£ŗ¢Łµ±0£¼t£¼2Ź±£¬ÓŠ4t£ŗ£Ø12©4t£©=1£ŗ3£¬½āµĆt= ![]() £®
£®
¢Śµ±2£¼t£¼4Ź±£¬ÓŠ£Ø©t2+8t©4£©£ŗ[12©£Ø©t2+8t©4£©]=3£ŗ1£¬
¼“t2©8t+13=0£¬
½āµĆt=4© ![]() £¬t=4+
£¬t=4+ ![]() £ØÉįČ„£©£®
£ØÉįČ„£©£®
µ±t= ![]() »ņt=4©
»ņt=4© ![]() Ź±£¬Ö±Ļßl½«Ö±½ĒĢŻŠĪABCD·Ö³ÉµÄĮ½²æ·ÖĆ껿֮±ČĪŖ1£ŗ3
Ź±£¬Ö±Ļßl½«Ö±½ĒĢŻŠĪABCD·Ö³ÉµÄĮ½²æ·ÖĆ껿֮±ČĪŖ1£ŗ3
”¾½āĪö”æ½ā£ŗÓÉĢāŅāµĆ£ŗ£Ø1£©AB=2£®£Ø2£©SĢŻŠĪABCD=12£®
£Ø1£©øł¾ŻĶ¼¢ŚæÉÖŖ£¬µ±0”Üt”Ü2Ź±£¬EŌŚĻ߶ĪABÉĻŌĖ¶Æ£Ø°üĄØÓėA”¢BÖŲŗĻ£©£¬ŌŚ“ĖĘŚ¼äEµćŌĖ¶ÆĮĖ2£¬Ņņ“ĖæÉĒóµĆABµÄ³¤ĪŖ2£®£Ø2£©øł¾ŻĶ¼ŠĪæÉÖŖ£ŗµ±2£¼t£¼4Ź±£¬EŌŚABµÄŃÓ³¤ĻßÉĻ£¬ĒŅFŌŚDµć×ó²ą£¬“ĖĘŚ¼äEµćŌĖ¶ÆĮĖ2£¬Ņņ“ĖĻĀµ×³¤ĪŖ2+2=4£¬øł¾Żt=2Ź±£¬ÖŲŗĻ²æ·ÖµÄĆ껿ĪŖ8æÉĒó³öĢŻŠĪµÄøßĪŖ4£¬Ņņ“ĖĢŻŠĪµÄĆ껿ĪŖ ![]() ”Į£Ø2+4£©”Į4=12£®£Ø3£©µ±t£¾4Ź±£¬Ö±ĻßlÓėĢŻŠĪƻӊ½»µć£¬Ņņ“ĖÉعżµÄĆ껿ŗćĪŖĢŻŠĪµÄĆ껿12£®£Ø4£©µ±2£¼t£¼4Ź±£¬Ö±ĻßÉعżĢŻŠĪµÄ²æ·ÖŹĒøöĪå±ßŠĪ£¬Čē¹ūÉčÖ±ĻßlÓėADµÄ½»µćĪŖ0£¬ÄĒĆ“ÖŲŗĻ²æ·ÖµÄĆ껿æÉÓĆĢŻŠĪµÄĆ껿¼õČ„Čż½ĒŠĪOFDµÄĆ껿Ą“ĒóµĆ£®ĢŻŠĪµÄĆ껿ŌŚ£Ø2£©ÖŠŅŃ¾ĒóµĆ£®Čż½ĒŠĪOFDÖŠ£¬µ×±ßDF=4©t£¬¶ųDFÉĻµÄøߣ¬æÉÓĆDFµÄ³¤ŗĶ”ĻBCDµÄÕżĒŠÖµĒó³ö£¬ÓÉ“ĖæÉµĆ³öS£¬tµÄŗÆŹż¹ŲĻµŹ½£®£Ø5£©±¾ĢāŅŖ·ÖĒéæöĢÖĀŪ£ŗ¢Łµ±0£¼t£¼2Ź±£¬ÖŲŗĻ²æ·ÖµÄĘ½ŠŠĖıߊĪµÄĆ껿£ŗÖ±½ĒĢŻŠĪAEFDµÄĆ껿=1£ŗ3£¬¾Ż“ĖæÉĒó³ötµÄÖµ£®¢Śµ±2£¼t£¼4Ź±£¬ÖŲŗĻ²æ·ÖµÄĪå±ßŠĪµÄĆ껿£ŗČż½ĒŠĪOFDµÄĆ껿=3£ŗ1£¬ÓÉ“ĖæÉĒó³ötµÄÖµ£®
”Į£Ø2+4£©”Į4=12£®£Ø3£©µ±t£¾4Ź±£¬Ö±ĻßlÓėĢŻŠĪƻӊ½»µć£¬Ņņ“ĖÉعżµÄĆ껿ŗćĪŖĢŻŠĪµÄĆ껿12£®£Ø4£©µ±2£¼t£¼4Ź±£¬Ö±ĻßÉعżĢŻŠĪµÄ²æ·ÖŹĒøöĪå±ßŠĪ£¬Čē¹ūÉčÖ±ĻßlÓėADµÄ½»µćĪŖ0£¬ÄĒĆ“ÖŲŗĻ²æ·ÖµÄĆ껿æÉÓĆĢŻŠĪµÄĆ껿¼õČ„Čż½ĒŠĪOFDµÄĆ껿Ą“ĒóµĆ£®ĢŻŠĪµÄĆ껿ŌŚ£Ø2£©ÖŠŅŃ¾ĒóµĆ£®Čż½ĒŠĪOFDÖŠ£¬µ×±ßDF=4©t£¬¶ųDFÉĻµÄøߣ¬æÉÓĆDFµÄ³¤ŗĶ”ĻBCDµÄÕżĒŠÖµĒó³ö£¬ÓÉ“ĖæÉµĆ³öS£¬tµÄŗÆŹż¹ŲĻµŹ½£®£Ø5£©±¾ĢāŅŖ·ÖĒéæöĢÖĀŪ£ŗ¢Łµ±0£¼t£¼2Ź±£¬ÖŲŗĻ²æ·ÖµÄĘ½ŠŠĖıߊĪµÄĆ껿£ŗÖ±½ĒĢŻŠĪAEFDµÄĆ껿=1£ŗ3£¬¾Ż“ĖæÉĒó³ötµÄÖµ£®¢Śµ±2£¼t£¼4Ź±£¬ÖŲŗĻ²æ·ÖµÄĪå±ßŠĪµÄĆ껿£ŗČż½ĒŠĪOFDµÄĆ껿=3£ŗ1£¬ÓÉ“ĖæÉĒó³ötµÄÖµ£®



| Äź¼¶ | øßÖŠæĪ³Ģ | Äź¼¶ | ³õÖŠæĪ³Ģ |
| øßŅ» | øßŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” | ³õŅ» | ³õŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” |
| ø߶ž | ø߶žĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õ¶ž | ³õ¶žĆā·ŃæĪ³ĢĶĘ¼ö£” |
| øßČż | øßČżĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õČż | ³õČżĆā·ŃæĪ³ĢĶĘ¼ö£” |
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æŌŚ”÷ABCÖŠ£¬AB=AC£¬µćDŹĒÖ±ĻßBCÉĻŅ»µć£Ø²»ÓėB”¢CÖŲŗĻ£©£¬ŅŌADĪŖŅ»±ßŌŚADµÄÓŅ²ą×÷”÷ADE£¬Ź¹AD=AE£¬”ĻDAE=”ĻBAC£¬Į¬½ÓCE£®
£Ø1£©ČēĶ¼1£¬µ±µćDŌŚĻ߶ĪBCÉĻ£¬Čē¹ū”ĻBAC=90”ć£¬Ōņ”ĻBCE=_______¶Č£»
£Ø2£©ČēĶ¼2Čē¹ū”ĻBAC=60”ć£¬Ōņ”ĻBCE=______¶Č£»
£Ø3£©Éč”ĻBAC=![]() £¬”ĻBCE=
£¬”ĻBCE=![]() £®
£®
¢ŁČēĶ¼3£¬µ±µćDŌŚĻ߶ĪBCÉĻŅĘ¶Æ£¬Ōņ![]() Ö®¼äÓŠŌõŃłµÄŹżĮæ¹ŲĻµ£æĒėĖµĆ÷ĄķÓÉ£»
Ö®¼äÓŠŌõŃłµÄŹżĮæ¹ŲĻµ£æĒėĖµĆ÷ĄķÓÉ£»
¢Śµ±µćDŌŚÖ±ĻßBCÉĻŅĘ¶Æ£¬ĒėÖ±½ÓŠ“³ö![]() ֮ѳµÄŹżĮæ¹ŲĻµ£¬²»ÓĆÖ¤Ć÷”£
֮ѳµÄŹżĮæ¹ŲĻµ£¬²»ÓĆÖ¤Ć÷”£




²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
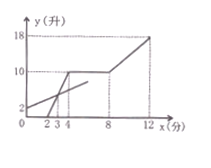
”¾ĢāÄæ”æĻÖÓŠ¼×”¢ŅŅĮ½øöČŻĘ÷£¬·Ö±š×°ÓŠ½ųĖ®¹ÜŗĶ³öĖ®¹Ü £¬Į½ČŻĘ÷µÄ½ų³öĖ®ĖŁ¶Č²»±ä£¬ĻČ“ņæŖŅŅČŻĘ÷µÄ½ųĖ®¹Ü£¬2·ÖÖÓŹ±ŌŁ“ņæŖ¼×ČŻĘ÷µÄ½ųĖ®¹Ü£¬ÓÖ¹ż2·ÖÖÓ¹Ų±Õ¼×ČŻĘ÷µÄ½ųĖ®¹Ü£¬ŌŁ¹ż4·ÖÖÓĶ¬Ź±“ņæŖ¼×ČŻĘ÷µÄ½ų”¢³öĖ®¹Ü”£Ö±µ½12·ÖÖÓŹ±£¬Ķ¬Ź±¹Ų±ÕĮ½ČŻĘ÷µÄ½ų³öĖ®¹Ü”£“ņæŖŗĶ¹Ų±ÕĖ®¹ÜµÄŹ±¼äŗöĀŌ²»¼Ę”£ČŻĘ÷ÖŠµÄĖ®Įæy(Éż)ÓėŅŅČŻĘ÷×¢Ė®Ź±¼äx(·Ö)Ö®¼äµÄ¹ŲĻµČēĶ¼ĖłŹ¾
£Ø1£©Ēó¼×ČŻĘ÷µÄ½ų”¢³öĖ®ĖŁ¶Č£»
£Ø2£©µ±![]() Ź±£¬ŌŚÕā¹ż³ĢÖŠŹĒ·ń“ęŌŚĮ½ČŻĘ÷µÄĖ®ĮæĻąµČ£æČō“ęŌŚ£¬Ēó³ö“ĖŹ±xµÄÖµ£»
Ź±£¬ŌŚÕā¹ż³ĢÖŠŹĒ·ń“ęŌŚĮ½ČŻĘ÷µÄĖ®ĮæĻąµČ£æČō“ęŌŚ£¬Ēó³ö“ĖŹ±xµÄÖµ£»
£Ø3£©Čē¹ūŌŚŅŅČŻĘ÷ÖŠŌŁ×°Ņ»øö½ųĖ®¹Ü£¬Ęä½ųĖ®ĖŁ¶ČŹĒ2Éż£Æ·Ö£¬ČōŹ¹Į½ČŻĘ÷µŚ12·ÖÖÓŹ±µÄĖ®ĮæĻąµČ £¬ŌņÓ¦øĆŌŚµŚ¼ø·ÖÖÓ“ņæŖ“Ė½ųĖ®¹Ü£æ
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬ŌŚĖıߊĪABCDÖŠ£¬AD”ĪBC£¬”ĻA=90”ć£¬CE”ĶBDÓŚE£¬AB=EC 
£Ø1£©ĒóÖ¤£ŗ”÷ABD”Õ”÷ECB£»
£Ø2£©Čō”ĻEDC=65”ć£¬Ēó”ĻECBµÄ¶ČŹż£»
£Ø3£©ČōAD=3£¬AB=4£¬ĒóDCµÄ³¤£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬ŌŚĘ½ĆęÖ±½Ē×ų±źĻµÖŠ,A”¢B¾łŌŚ±ß³¤ĪŖ1µÄÕż·½ŠĪĶųøńøńµćÉĻ£®

£Ø1£©ŌŚĶųøńµÄøńµćÖŠ,ŅŌABĪŖ±ß»Ņ»øö”÷ABC£¬Ź¹Čż½ĒŠĪĮķĶāĮ½±ß³¤ĪŖ![]() ”¢
”¢![]() £»
£»
£Ø2£©ČōµćPŌŚĶ¼ÖŠĖłøųĶųøńÖŠµÄøńµćÉĻ£¬”÷APBŹĒµČŃüČż½ĒŠĪ£¬Āś×ćĢõ¼žµÄµćP¹²ÓŠ øö£»
£Ø3£©Čō½«Ļ߶ĪABČʵćAĖ³Ź±ÕėŠż×Ŗ90”ć£¬Š“³öŠż×ŖŗóµćBµÄ×ų±ź .
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æ¼ĘĖć»ņ½ā·½³Ģ
£Ø1£©©14+£Ø©5£©2”Į£Ø©![]() £©+|0.8©1|
£©+|0.8©1|
£Ø2£©©1.53”Į0.75+1.53”Į![]() +
+![]() ”Į1.53
”Į1.53
£Ø3£©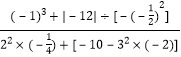
£Ø4£©![]() £®
£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æĪŅĆĒ¹ę¶Ø£ŗ![]() £½
£½![]() £Øa”Ł0£©£¬¼“aµÄøŗP“ĪĆŻµČÓŚaµÄp“ĪĆŻµÄµ¹Źż£®Ąż£ŗ
£Øa”Ł0£©£¬¼“aµÄøŗP“ĪĆŻµČÓŚaµÄp“ĪĆŻµÄµ¹Źż£®Ąż£ŗ![]() £½
£½![]()
£Ø1£©¼ĘĖć£ŗ![]() £½__£»
£½__£»![]() £½__£»
£½__£»
£Ø2£©Čē¹ū![]() £½
£½![]() £¬ÄĒĆ“p£½__£»Čē¹ū
£¬ÄĒĆ“p£½__£»Čē¹ū![]() £½
£½![]() £¬ÄĒĆ“a£½__£»
£¬ÄĒĆ“a£½__£»
£Ø3£©Čē¹ū![]() £½
£½![]() £¬ĒŅa”¢pĪŖÕūŹż£¬ĒóĀś×ćĢõ¼žµÄa”¢pµÄȔֵ£®
£¬ĒŅa”¢pĪŖÕūŹż£¬ĒóĀś×ćĢõ¼žµÄa”¢pµÄȔֵ£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬ŌŚĘ½ĆęÖ±½Ē×ų±źĻµÖŠÓŠŅ»øöÖį¶Ō³ĘĶ¼ŠĪ£¬A£Ø3£¬-2£©£¬B£Ø3£¬©6£©Į½µćŌŚ“ĖĶ¼ŠĪÉĻĒŅ»„ĪŖ¶Ō³Ęµć£¬Čō“ĖĶ¼ŠĪÉĻÓŠŅ»øöµćC£Ø©2£¬+1£©£®
£Ø1£©ĒóµćCµÄ¶Ō³ĘµćµÄ×ų±ź£®
£Ø2£©Ēó”÷ABCµÄĆ껿£®

²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬Ö±Ļßy=©![]() x+8ÓėxÖį£¬yÖį·Ö±š½»ÓŚµćAŗĶB£¬MŹĒOBÉĻµÄŅ»µć£¬Čō½«”÷ABMŃŲAMÕŪµž£¬µćBĒ”ŗĆĀäŌŚxÖįÉĻµÄµćB”䓦£¬ŌņÖ±ĻßAMµÄ½āĪöŹ½ĪŖ ”” £®
x+8ÓėxÖį£¬yÖį·Ö±š½»ÓŚµćAŗĶB£¬MŹĒOBÉĻµÄŅ»µć£¬Čō½«”÷ABMŃŲAMÕŪµž£¬µćBĒ”ŗĆĀäŌŚxÖįÉĻµÄµćB”䓦£¬ŌņÖ±ĻßAMµÄ½āĪöŹ½ĪŖ ”” £®

²éæ““š°øŗĶ½āĪö>>
°Ł¶ČÖĀŠÅ - Į·Ļ°²įĮŠ±ķ - ŹŌĢāĮŠ±ķ
ŗž±±Ź”»„ĮŖĶųĪ„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±ØĘ½ĢØ | ĶųÉĻÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | µēŠÅÕ©Ę¾Ł±Ø×ØĒų | É꥜Ź·ŠéĪŽÖ÷ŅåÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | ÉęĘóĒÖČؾŁ±Ø×ØĒų
Ī„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±Øµē»°£ŗ027-86699610 ¾Ł±ØÓŹĻä£ŗ58377363@163.com