
【题目】如图,反比例函数![]() 的图象经过点A(4,b),过点A作AB⊥x轴于点B,△AOB的面积为2.
的图象经过点A(4,b),过点A作AB⊥x轴于点B,△AOB的面积为2.
(1)求k和b的值;
(2)若一次函数y=ax﹣3的图象经过点A,求这个一次函数的解析式.

【答案】(1)k=4,b=1;(2)y=x﹣3
【解析】
(1)由△AOB的面积为2,根据反比例函数的比例系数k的几何意义,可知k的值,得出反比例函数的解析式,然后把x=4代入,即可求出b的值;
(2)把点A的坐标代入y=ax﹣3,即可求出这个一次函数的解析式.
解:(1)∵反比例函数![]() 的图象经过点A,AB⊥x轴于点B,△AOB的面积为2,A(4,b),
的图象经过点A,AB⊥x轴于点B,△AOB的面积为2,A(4,b),
∴![]() OB×AB=2,∴
OB×AB=2,∴![]() ×4×b=2,
×4×b=2,
∴AB=b=1,
∴A(4,1),
∴k=xy=4,
∴反比例函数的解析式为y=![]() ,
,
即k=4,b=1.
(2)∵A(4,1)在一次函数y=ax﹣3的图象上,
∴1=4a﹣3,
∴a=1.
∴这个一次函数的解析式为y=x﹣3.


 教材全解字词句篇系列答案
教材全解字词句篇系列答案科目:初中数学 来源: 题型:
【题目】如图,要建一个长方形养鸡场,鸡场的一边靠墙,如果用50m长的篱笆围成中间有一道篱笆隔墙的养鸡场,设它的长度为x m.
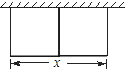
(1)要使鸡场面积最大,鸡场的长度应为多少m?
(2)如果中间有n(n是大于1的整数)道篱笆隔墙,要使鸡场面积最大,鸡场的长应为多少m?
比较(1)(2)的结果,你能得到什么结论?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,BD⊥AC,对角线AC所在的直线上有两点M、N,使∠MBN=135°,若AD=4,AM=3,则CN的长是_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两个袋中均装有三张除所标数值外完全相同的卡片,甲袋中的三张卡片上所标有的三个数值为﹣7,﹣1,3.乙袋中的三张卡片所标的数值为﹣2,1,6.先从甲袋中随机取出一张卡片,用x表示取出的卡片上的数值,再从乙袋中随机取出一张卡片,用y表示取出卡片上的数值,把x、y分别作为点A的横坐标和纵坐标.
(1)用适当的方法写出点A(x,y)的所有情况.
(2)求点A落在第三象限的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
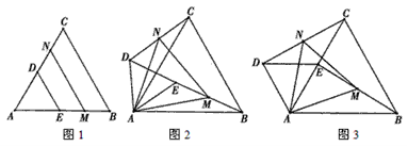
【题目】如图,若△ABC和△ADE为等边三角形,M,N分别EB,CD的中点,易证:CD=BE,△AMN是等边三角形.
(1)当把△ADE绕A点旋转到图2的位置时,CD=BE是否仍然成立?若成立请证明,若不成立请说明理由;
(2)当△ADE绕A点旋转到图3的位置时,△AMN是否还是等边三角形?若是,请给出证明;若不是,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“扬州漆器”名扬天下,某网店专门销售某种品牌的漆器笔筒,成本为30元/件,每天销售量![]() (件)与销售单价
(件)与销售单价![]() (元)之间存在一次函数关系,如图所示.
(元)之间存在一次函数关系,如图所示.
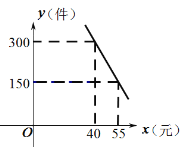
(1)求![]() 与
与![]() 之间的函数关系式;
之间的函数关系式;
(2)如果规定每天漆器笔筒的销售量不低于240件,当销售单价为多少元时,每天获取的利润最大,最大利润是多少?
(3)该网店店主热心公益事业,决定从每天的销售利润中捐出150元给希望工程,为了保证捐款后每天剩余利润不低于3600元,试确定该漆器笔筒销售单价的范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一天早晨,小玲从家出发匀速步行到学校,小玲出发一段时间后,她的妈妈发现小玲忘带了一件必需的学习用品,于是立即下楼骑自行车,沿小玲行进的路线,匀速去追小玲,妈妈追上小玲将学习用品交给小玲后,立即沿原路线匀速返回家里,但由于路上行人渐多,妈妈返回时骑车的速度只是原来速度的一半,小玲继续以原速度步行前往学校,妈妈与小玲之间的距离y(米)与小玲从家出发后步行的时间x(分)之间的关系如图所示(小玲和妈妈上、下楼以及妈妈交学习用品给小玲耽搁的时间忽略不计).当妈妈刚回到家时,小玲离学校的距离为_____米.
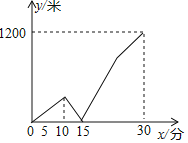
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com