НтД№ЃК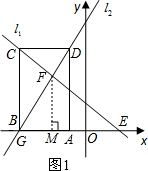
НтЃКЃЈ1ЃЉгЩЬтвтЕУ
ЃЌ
НтЕУx=-2ЃЌy=4ЃЌ
ЁрFЕузјБъЃКЃЈ-2ЃЌ4ЃЉЃЛ
Й§FЕузїжБЯпFMДЙжБXжсНЛxжсгкMЃЌME=MF=4ЃЌЁїMEFЪЧЕШбќжБНЧШ§НЧаЮЃЌЁЯGEF=45ЁуЃЛ
ЃЈ2ЃЉЁпЕуGЪЧжБЯпl2гыxжсЕФНЛЕуЃЌ
ЁрЕБy=0ЪБЃЌ2x+8=0ЃЌНтЕУx=-4ЃЌ
ЁрGЕуЕФзјБъЮЊЃЈ-4ЃЌ0ЃЉЃЌдђCЕуЕФКсзјБъЮЊ-4ЃЌ
ЁпЕуCдкжБЯпl
1ЩЯЃЌ
ЁрЕуCЕФзјБъЮЊЃЈ-4ЃЌ6ЃЉЃЌ
ЁпгЩЭМПЩжЊЕуDгыЕуCЕФзнзјБъЯрЭЌЃЌЧвЕуDдкжБЯпl
2ЩЯЃЌ
ЁрЕуDЕФзјБъЮЊЃЈ-1ЃЌ6ЃЉЃЌ
ЁпгЩЭМПЩжЊЕуAгыЕуDЕФКсзјБъЯрЭЌЃЌЧвЕуAдкxжсЩЯЃЌ
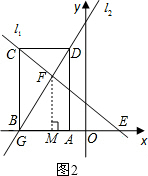
ЁрЕуAЕФзјБъЮЊЃЈ-1ЃЌ0ЃЉЃЌ
ЁрDC=|-1-ЃЈ-4ЃЉ|=3ЃЌBC=6ЃЛ
ЃЈ3ЃЉЁпЕуEЪЧl
1гыxжсЕФНЛЕуЃЌ
ЁрЕуEЕФзјБъЮЊЃЈ2ЃЌ0ЃЉЃЌ
S
ЁїGFE=
GE•MF=
(2+4)ЁС4=12ЃЌ
ШєОиаЮABCDДгдЕиГіЗЂЃЌбиxжсе§ЗНЯђвдУПУы1ИіЕЅЮЛГЄЖШЕФЫйЖШЦНвЦЃЌ
ЕБtУыЪБЃЌвЦЖЏЕФОрРыЪЧ1ЁСt=tЃЌдђBЕуЕФзјБъЮЊЃЈ-4+tЃЌ0ЃЉЃЌAЕуЕФзјБъЮЊЃЈ-1+tЃЌ0ЃЉЃЛ
ЂйдкдЫЖЏЕНtУыЃЌШєBCБпгыl
2ЯрНЛЩшНЛЕуЮЊNЃЌADгыl
1ЯрНЛЩшНЛЕуЮЊKЃЌФЧУД-4Ём-4+tЁм-2ЃЌМД0ЁмtЁм2ЪБЃЎ
NЕуЕФзјБъЮЊЃЈ-4+tЃЌ2tЃЉЃЌKЕуЕФзјБъЮЊЃЈ-1+tЃЌ3-tЃЉЃЌ
s=S
ЁїGFE-S
ЁїGNB-S
ЁїAEK=12-
t•2t-(3-t)•(3-t)=-
t2-3t+ЃЌ
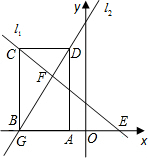
ЂкдкдЫЖЏЕНtУыЃЌШєBCБпгыl
1ЯрНЛЩшНЛЕуЮЊNЃЌADгыl
1ЯрНЛЩшНЛЕуЮЊKЃЌФЧУД-2ЃМ-4+tЧв-1+tЁм3ЃЌМД2ЃМtЃМ4ЪБЃЎ
NЕуЕФзјБъЮЊЃЈ-4+tЃЌ6-tЃЉЃЌKЕуЕФзјБъЮЊЃЈ-1+tЃЌ3-tЃЉЃЌ
s=S
ЬнаЮBNKA=
[(6-t)+(3-t)]•3=
- 3t+ЃЌ
ЂлдкдЫЖЏЕНtУыЃЌШєBCБпгыl
1ЯрНЛЩшНЛЕуЮЊNЃЌADгыl
1ВЛЯрНЛЃЌФЧУД-4+tЁм3Чв-1+tЃО3ЃЌМД4ЁмtЁм6ЪБЃЎ
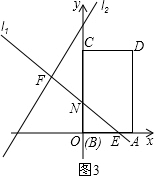
NЕуЕФзјБъЮЊЃЈ-4+tЃЌ6-tЃЉЃЌ
s=S
ЁїBNE=
[2-(-4+t)]•(6-t)=
t2-6t+18ЃЌ
Д№ЃКЃЈ1ЃЉFЕузјБъЃКЃЈ-2ЃЌ4ЃЉЃЌЁЯGEFЕФЖШЪ§ЪЧ45ЁуЃЛ
ЃЈ2ЃЉОиаЮABCDЕФБпDCЕФГЄЮЊ3ЃЌBCЕФГЄЮЊ6ЃЛ
ЃЈ3ЃЉsЙигкtЕФКЏЪ§ЙиЯЕЪН
| | s=-t2-3t+(0ЁмtЁм2) | | s=-3t+(2ЃМtЃМ4) | | s=t2-6t+18(4ЁмtЁм6) |
| |
ЃЎ

 CDЖЅЕуCЁЂDЗжБ№дкжБЯпl1ЁЂl2ЃЌЖЅЕуAЁЂBЖМдкxжсЩЯЃЌЧвЕуBгыЕуGжиКЯЃЎ
CDЖЅЕуCЁЂDЗжБ№дкжБЯпl1ЁЂl2ЃЌЖЅЕуAЁЂBЖМдкxжсЩЯЃЌЧвЕуBгыЕуGжиКЯЃЎ НтЃКЃЈ1ЃЉгЩЬтвтЕУ
НтЃКЃЈ1ЃЉгЩЬтвтЕУ




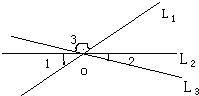 6ЁЂШчЭМЃЌвбжЊжБЯпl1ЃЌl2ЃЌl3ЯрНЛгкЕуOЃЌЁЯ1=35ЁуЃЌЁЯ2=25ЁуЃЌдђЁЯ3ЕШгкЃЈЁЁЁЁЃЉ
6ЁЂШчЭМЃЌвбжЊжБЯпl1ЃЌl2ЃЌl3ЯрНЛгкЕуOЃЌЁЯ1=35ЁуЃЌЁЯ2=25ЁуЃЌдђЁЯ3ЕШгкЃЈЁЁЁЁЃЉ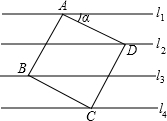 ЃЈ2012•лАГЧЯивЛФЃЃЉШчЭМЃЌвбжЊжБЯпl1ЁЮl2ЁЮl3ЁЮl4ЃЌЯрСкСНЬѕЦНаажБЯпМфЕФОрРыЖМЪЧ1ЃЌШчЙће§ЗНаЮABCDЕФЫФИіЖЅЕуЗжБ№дкЫФЬѕжБЯпЩЯЃЌдђcosІС=ЃЈЁЁЁЁЃЉ
ЃЈ2012•лАГЧЯивЛФЃЃЉШчЭМЃЌвбжЊжБЯпl1ЁЮl2ЁЮl3ЁЮl4ЃЌЯрСкСНЬѕЦНаажБЯпМфЕФОрРыЖМЪЧ1ЃЌШчЙће§ЗНаЮABCDЕФЫФИіЖЅЕуЗжБ№дкЫФЬѕжБЯпЩЯЃЌдђcosІС=ЃЈЁЁЁЁЃЉ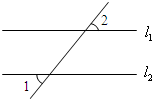 ЃЈ2007•ЧФЯжнЃЉШчЭМЃЌвбжЊжБЯпl1ЁЮl2ЃЌЁЯ1=50ЁуЃЌФЧУДЁЯ2=
ЃЈ2007•ЧФЯжнЃЉШчЭМЃЌвбжЊжБЯпl1ЁЮl2ЃЌЁЯ1=50ЁуЃЌФЧУДЁЯ2=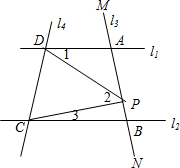 ШчЭМЃКвбжЊжБЯпl1ЁЮl2ЃЌЧвl3ЁЂl4КЭl1ЁЂl2ЗжБ№НЛгкЕуAЁЂBКЭЕуCЁЂDЃЌЕуPдкABЩЯЃЌЩшЁЯADP=ЁЯ1ЃЌЁЯDPC=ЁЯ2ЃЌЁЯBCP=ЁЯ3ЃЎ
ШчЭМЃКвбжЊжБЯпl1ЁЮl2ЃЌЧвl3ЁЂl4КЭl1ЁЂl2ЗжБ№НЛгкЕуAЁЂBКЭЕуCЁЂDЃЌЕуPдкABЩЯЃЌЩшЁЯADP=ЁЯ1ЃЌЁЯDPC=ЁЯ2ЃЌЁЯBCP=ЁЯ3ЃЎ ШчЭМЃЌвбжЊжБЯпl1ЁЮl2ЃЌжБЯпl3КЭжБЯпl1ЁЂl2НЛгкЕуCКЭDЃЌдкжБЯпl3ЩЯгаЕуPЃЈЕуPгыЕуCЁЂDВЛжиКЯЃЉЃЌЕуAдкжБЯпl1ЩЯЃЌЕуBдкжБЯпl2ЩЯЃЎ
ШчЭМЃЌвбжЊжБЯпl1ЁЮl2ЃЌжБЯпl3КЭжБЯпl1ЁЂl2НЛгкЕуCКЭDЃЌдкжБЯпl3ЩЯгаЕуPЃЈЕуPгыЕуCЁЂDВЛжиКЯЃЉЃЌЕуAдкжБЯпl1ЩЯЃЌЕуBдкжБЯпl2ЩЯЃЎ