
��ͼ����ƽ��ֱ������ϵ�У�������y=x2+bx+c�����㣨1����1�����ҶԳ���Ϊ����x=2����P��Q�����������ϣ���Pλ�ڶԳ����Ҳ࣬��Qλ�ڶԳ�����࣬PA��ֱ�Գ����ڵ�A��QB��ֱ�Գ����ڵ�B����QB=PA+1�����P�ĺ�����Ϊm��
��1������������������Ӧ�ĺ�����ϵʽ��
��2�����Q�����꣨�ú�m��ʽ�ӱ�ʾ����
��3����̽��PA+QB=AB�Ƿ��������˵�����ɣ�
��4��������y=a1x2+b1x+c1��a1��0������Q��B��P���㣬����Գ�����ı���PAQB�ֳ����Ϊ1��5�������֣�ֱ��д����ʱm��ֵ��
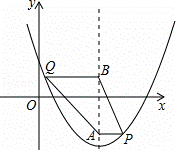
�⣺��1����������y=x2+bx+c�����㣨1����1�����ҶԳ���Ϊ����x=2��
��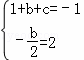 ��
��
���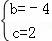 ��
��
����������������Ӧ�ĺ�����ϵʽy=x2��4x+2��
��2�����������ϵ�P�ĺ�����Ϊm��
��P��m��m2��4m+2����
��PA=m��2��
QB=PA+1=m��2+1=m��1��
���Q�ĺ�����Ϊ2����m��1��=3��m��
��Q����������3��m��2��4��3��m��+2=m2��2m��1��
���Q��������3��m��m2��2m��1����
��3��PA+QB=AB������
�������£���P��m��m2��4m+2����Q��3��m��m2��2m��1����
��A��2��m2��4m+2����B��2��m2��2m��1����
��AB=��m2��2m��1������m2��4m+2��=2m��3��
�֡�PA=m��2��QB=m��1��
��PA+QB=m��2+m��1=2m��3��
��PA+QB=AB��
��4����������y=a1x2+b1x+c1��a1��0������Q��B��P���㣬
��������y=a1x2+b1x+c1�ĶԳ���ΪQB�Ĵ�ֱƽ���ߣ�
�߶Գ�����ı���PAQB�ֳ����Ϊ1��5�������֣�
��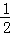 ��
��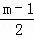 ��
��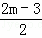 =
=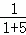 ��
��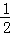 ��2m��3������2m��3����
��2m��3������2m��3����
�������2m��3����m��3��=0��
�ߵ�Pλ�ڶԳ����Ҳ࣬
��m��2��
��2m��3��0��
��m��3=0��
���m=3��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
������̰������ѧ�̲���ʹ�õ�ij�ּ��������м��㣬���Ľ��Ϊ��������

| �� | A�� | 21 | B�� | 15 | C�� | 84 | D�� | 67 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
��ͼ��������ABCD�У�AD��BC����ADC=90�㣬��B=30�㣬CE��AB������Ϊ��E����AD=1��AB=2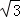 ����CE�ij���
����CE�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
��ͼ���ڡ�ABC�У���C=90�㣬AB=10��AD�ǡ�ABC��һ����ƽ���ߣ���CD=3�����ABD�����Ϊ������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
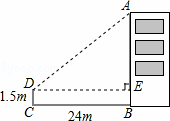
��ͼ��Ϊ����ij������ĸ߶�AB������ý�����ײ�24�ĵ�C����Ŀ�⽨���ﶥ��A����������ˮƽ�нǡ�ADEΪ39�㣬�Ҹ�CDΪ1.5�ף�������ĸ߶�AB���������ȷ��0.1�ף����ο����ݣ�sin39��=0.63��cos39��=0.78��tan39��=0.81��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
Ϊӭ�ӡ�2014������Ѽ�̽�����������������������������Ͷ��Լ4000��Ԫ�����̻�����.4000���ÿ�ѧ��������ʾΪ
A. 4��106 B. 4��107  C. 4��108 D. 0.4��107
C. 4��108 D. 0.4��107
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
��һ�������Ŀڴ��У�װ�����ɸ�����ɫ��ͬ�����ͬ��������ڴ���װ�У�����������������ĸ���Ϊ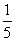 ����ô�ڴ�������ܸ���Ϊ_
����ô�ڴ�������ܸ���Ϊ_ ___________.
___________.
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com