练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

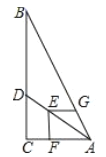
    【题目】如图，在 RtABC 中， ACB 90 ， AC 6 ， BC 12 ，点 D 在边 BC 上，点 E在线段 AD 上， EF AC 于点 F ， EG EF 交 AB 于点 G ．若 EF EG ，则 CD 的长为____________

    【答案】4

    【解析】

    根据题意和三角形相似的判定和性质，即可以求得CD的长．

    解：作DH∥EG交AB于点H，则△AEG∽△ADH，


    ∴，
    ∵EF⊥AC，∠C=90°，
    ∴∠EFA=∠C=90°，
    ∴EF∥CD，
    ∴△AEF∽△ADC，
    ∴，
    ∴，
    ∵EG=EF，
    ∴DH=CD，
    设DH=x，则CD=x，
    ∵BC=12，AC=6，
    ∴BD=12-x，
    ∵EF⊥AC，EF⊥EG，DH∥EG，
    ∴EG∥AC∥DH，
    ∴△BDH∽△BCA，
    ∴，
    即，
    解得，x=4，
    ∴CD=4，
    故答案为4．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】把一根长为米的铁丝折成一个矩形，矩形的一边长为米，面积为S米，

    (1)求S关于的函数表达式和的取值范围

    (2)为何值时，S最大？最大为多少？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】装潢公司要给边长为6米的正方形墙面ABCD进行装潢，设计图案如图所示（四周是四个全等的矩形，用材料甲进行装潢；中心区是正方形MNPQ，用材料乙进行装潢）．

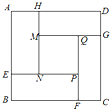
    两种装潢材料的成本如下表：

    材料

    甲

    乙

    价格（元/米2）

    50

    40

    设矩形的较短边AH的长为x米，装潢材料的总费用为y元．

    （1）MQ的长为　 　米（用含x的代数式表示）；

    （2）求y关于x的函数解析式；

    （3）当中心区的边长不小于2米时，预备资金1760元购买材料一定够用吗？请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在平面直角坐标系xOy中，A（4，0），B（0，3），C（4，3），I是△ABC的内心，将△ABC绕原点逆时针旋转90°后，I的对应点I'的坐标为（　　）

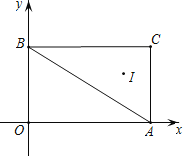
    A. （﹣2，3） B. （﹣3，2） C. （3，﹣2） D. （2，﹣3）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知关于的一元二次方程.

    （1）试证明：无论取何值此方程总有两个实数根；

    （2）若原方程的两根，满足，求的值.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知，如图，Rt△ABC 中，∠ACB=90°，BC=8，AC=6，点 D 在边 BC 上（不 与点 B、C 重合），点 E 在边 BC 的延长线上，∠DAE=∠BAC，点 F 在线段 AE 上，∠ACF=∠B．设 BD=x．

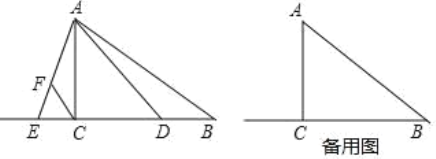
    （1）若点 F 恰好是 AE 的中点，求线段 BD 的长；

    （2）若 y=，求 y 关于 x 的函数关系式，并写出它的定义域；

    （3）当△ADE 是以 AD 为腰的等腰三角形时，求线段 BD 的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

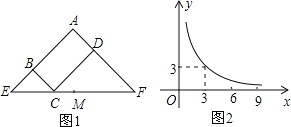
    【题目】如图1所示矩形中，，，与满足的反比例函数关系如图2所示，等腰直角三角形的斜边过点，点，分别在，上，为的中点，则下列结论正确的是（ ）

    A.当时，

    B.当时，

    C.当增大时，的值增大

    D.当增大时，的值不变

    查看答案和解析>>

    科目：初中数学 来源： 题型：

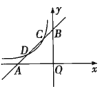
    【题目】如图，已知直线与x轴、y轴分别交于点A，B，与双曲线分别交于点C，D，且点C的坐标为.

    （1）分别求出直线、双曲线的函数表达式.

    （2）求出点D的坐标.

    （3）利用图象直接写出：当x在什么范围内取值时？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在平面直角坐标系中，点O（0，0），点A（1，0）．已知抛物线y＝x2+mx﹣2m（m是常数），顶点为P．

    （Ⅰ）当抛物线经过点A时，求顶点P的坐标；

    （Ⅱ）若点P在x轴下方，当∠AOP＝45°时，若函数值y＞0，求对应自变量x的取值范围；

    （Ⅲ）无论m取何值，该抛物线都经过定点H．当∠AHP＝45°时，求抛物线的解析式．

    查看答案和解析>>

    同步练习册答案