
分析 先根据一元二次方程x2-2(m+1)x+m2-2m-3=0有一根为0,求出m的值,然后把m的值代入x2-(k-m)x-k-m2+5m-2=0得到x2-(k-3)x-k+4=0,根据根的判别式求出k的取值范围,然后根据两个根x1,x2之差的绝对值为1求出k的值.
解答 解:∵关于x的一元二次方程x2-2(m+1)x+m2-2m-3=0的两个不相等的实数根中,有一个根为0,
∴△>0,△=4(m+1)2-4(m2-2m-3)=16m+16>0,即m>-1,
m2-2m-3=0,解得m1=-1,m2=3,
∴m=3,
∵方程x2-(k-m)x-k-m2+5m-2=0有两个根,
∴把m=3代入方程得x2-(k-3)x-k+4=0,
∴△=(k-3)2-4(4-k)=k2-2k-7=(k-1)2-8≥0,
k≥1+2$\sqrt{2}$或k≤1-2$\sqrt{2}$,
∵方程x2-(k-3)x-k+4=0的两个根分别是x1,x2,
∴x1+x2=k-3,x1•x2=4-k,
∴(x1-x2)2=(x1+x2)2-4x1•x2=(k-3)2-4(4-k)=k2-2k-7,
∵方程两个根x1,x2之差的绝对值为1,
∴k2-2k-7=1,解得k1=-2,k2=4,
∴存在实数k=-2或4时,使得x的方程x2-(k-m)x-k-m2+5m-2=0的两个根x1,x2之差的绝对值为1.
点评 本题主要考查了根与系数关系与根的判别式的知识,解答本题的关键是求出m的值,此题多次使用根的判别式,需要熟练掌握,此题难度不大.


 小学教材完全解读系列答案
小学教材完全解读系列答案科目:初中数学 来源: 题型:填空题
 甲、乙两人相距10千米,两人同时同向步行到A地,当甲到达A地后立即沿原路返回在途中与乙相遇,甲、乙两人的距离y(千米)与运动时间x(时)的关系如图所示,则乙出发前与A地的距离为19千米.
甲、乙两人相距10千米,两人同时同向步行到A地,当甲到达A地后立即沿原路返回在途中与乙相遇,甲、乙两人的距离y(千米)与运动时间x(时)的关系如图所示,则乙出发前与A地的距离为19千米.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
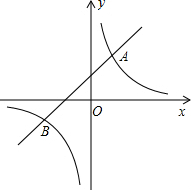 如图,已知一次函数y1=kx+b与反比例函数y2=$\frac{m}{x}$的图象交于A(2,4)、B(-4,n)两点.
如图,已知一次函数y1=kx+b与反比例函数y2=$\frac{m}{x}$的图象交于A(2,4)、B(-4,n)两点.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | -$\sqrt{3.6}$=-0.6 | B. | $\root{3}{-5}$=-$\root{3}{5}$ | C. | $\sqrt{(-13)^{2}}$=-13 | D. | $\sqrt{36}$=±6 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com