
����Ŀ��ij���е�һ����6000Ԫ�����ס���������Ʒ�����м���Ʒ������2��������Ʒ������3����20�����ס���������Ʒ�Ľ��ۺ��ۼ����±�(�����ۼ۩�����)��
�� | �� | |
����(Ԫ/��) | 20 | 28 |
�ۼ�(Ԫ/��) | 26 | 40 |
(1)�ó��е�һ�ι����ס���������Ʒ�ļ����ֱ��Ƕ��٣�
(2)�ó��н���һ�ι����ļס���������Ʒȫ��������һ���ɻ�ö�������
(3)�ó��еڶ�����ͬ���Ľ����ֹ����ס���������Ʒ�����м���Ʒ�����ǵ�һ�ε�2��������Ʒ�ļ������䣮����Ʒ��ԭ�����ۣ�����Ʒ�������ۣ��ڶ��μס���������Ʒ�������Ժ��õ�����ȵ�һ�λ�õ������560Ԫ����ڶ�������Ʒ�ǰ�ԭ�۴������۵ģ�
���𰸡�(1) �ó��е�һ�ι�������Ʒ160��������Ʒ100���� (2) �ɻ��2160Ԫ����(3) �ڶ�������Ʒ�ǰ�ԭ�۴�������۵�
��������
(1)��ó��е�һ�ι�������Ʒ![]() ��������Ʒ
��������Ʒ![]() ���������ܼ�=��������������������Ʒ������2��������Ʒ������3����20�������ɵó�����
���������ܼ�=��������������������Ʒ������2��������Ʒ������3����20�������ɵó�����![]() ��
��![]() �Ķ�Ԫһ�η����飬��֮���ɵó����ۣ�
�Ķ�Ԫһ�η����飬��֮���ɵó����ۣ�
(2)����������=ÿ����������������(��������)������������ۣ�
(3)��ڶ�������Ʒ�ǰ�ԭ�۴�m�����۵ģ�����������=ÿ����������������(��������)�����ɵó�����m��һԪһ�η��̣���֮���ɵó����ۣ�
(1)��ó��е�һ�ι�������Ʒ![]() ��������Ʒ
��������Ʒ![]() ����
����
�����⣬�ã�![]() ��
��
��ã�![]() ��
��
�𣺸ó��е�һ�ι�������Ʒ160��������Ʒ100����
(2)(26-20)��160+(40-28)��100=2160(Ԫ)��
�𣺸ó��н���һ�ι����ļס���������Ʒȫ��������һ���ɻ��2160Ԫ����
(3)��ڶ�������Ʒ�ǰ�ԭ�۴�m�����۵ģ�
�����⣬�ã�(26-20)��160��2+(40![]() -28)��100=2160+560��
-28)��100=2160+560��
���![]() ��
��
�𣺵ڶ�������Ʒ�ǰ�ԭ�۴�������۵ģ�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����������֤����
��֪����ͼ����D��E��F�ֱ����߶�AB��BC��AC�ϣ�����DE��EF��DMƽ�֡�ADE��EF�ڵ�M����1+��2=180�㣮
��֤�� ��B =��BED��

֤�����ߡ�1+��2=180�㣨��֪����
�֡ߡ�1+��BEM=180�㣨 ����
���2=��BEM�� ��������
��DM��______��_________________________________________����
���ADM =��B��_________________________________________����
��MDE =��BED��_______________________________________����
�֡�DMƽ�֡�ADE (��֪)��
���ADM =��MDE ( )��
���B =��BED��������������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��һö���ػ���ӵ���L�����䣬���������A��ʱ����λ�ھ��ܵײ�4km���ĵ����״�վR��LR=4����û���ײ�������Ϊ43�㣮1s�������B�㣬��ʱ��û���ײ�������Ϊ45.72�㣮��ö�����A��B��ƽ���ٶ��Ƕ��� �����ȡС�������λ����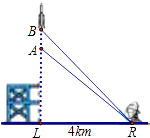
���ο����ݣ�sin43���0.682��cos43���0.731��tan43���0.933��
sin45.72���0.716��cos45.72���0.698��tan45.72���1.025��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����κ���y=ax2+bx+c��a��0����ͼ����ͼ��ʾ������˵����ȷ�ĸ����ǣ� ��
��a��0����b��0����c��0����b2��4ac��0����a+b+c=0��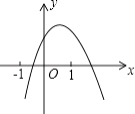
A.1
B.2
C.3
D.4
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����2015���ݣ�����Ħ�г���A��ȥB�أ��ҿ�������B��ȥA�أ�ͬʱ������������ʻ�����Ե����յ��ֹͣ����ס������˼����Ϊs����λ��ǧ�ף�������ʻ��ʱ��Ϊt����λ��Сʱ����s��t֮��ĺ�����ϵ��ͼ��ʾ�������н��ۣ�
�ٳ���1Сʱʱ���ס�����;��������
�ڳ���1.5Сʱʱ���ұȼ���ʻ��60ǧ�ף�
�۳���3Сʱʱ���ס���ͬʱ�����յ㣻
�ܼ��ٶ������ٶȵ�һ�룮
���У���ȷ���۵ĸ����ǣ�������

A. 4 B. 3 C. 2 D. 1
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����������������̣�
��ͼ����֪��1 ����2����B ����C�����Ƶ�AB��CD���������£�
�ߡ�1 ����2����֪����
�ҡ�1 ����CGD��______________________ ����
���2 ����CGD��������������
��CE��BF��___________________________����
��� ����C��__________________________����
�֡ߡ�B ����C����֪����
��� ����B��������������
��AB��CD��________________________________��.

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�����ı���ABCD�У�AD��BC����BAD=90�㣬�Խ���BD��DC��
��1����֤����ABD�ס�DCB��
��2�����AD=4��BC=9����BD�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪���κ���y=ax2+bx+c��ͼ�����A����1��0���͵�C��0��3�����Գ���Ϊֱ��x=1��
��1����ö��κ����Ĺ�ϵʽ�Ͷ������ꣻ
��2�����ͼ����������⣺
�ٵ���1��x��2ʱ������y��ȡֵ��Χ��
�ڵ�y��3ʱ����x��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ABC�У�AD�ǡ�BAC�Ľ�ƽ���ߣ�AE�ǡ�ABC�ĸߣ�

��1����ͼ1������B��40�㣬��C��62�㣬��˵����DAE�Ķ�����
��2����ͼ2����B����C������˵����DAE����B����C��������ϵ��
��3����ͼ3���ӳ�AC����F����CAE�͡�BCF�Ľ�ƽ���߽��ڵ�G�����G�Ķ�����
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com