
分析 先利用代入消元法求出方程组的解,再列出不等式组,然后求出两个不等式的解集,再求其公共解,最后根据k的取值范围写出正整数即可.
解答 解:$\left\{\begin{array}{l}{3x+y=2k①}\\{2y-x=3②}\end{array}\right.$,
由①得,y=-3x+2k③,
③代入②得,2(-3x+2k)-x=3,
解得x=$\frac{4k-3}{7}$,
将x=$\frac{4k-3}{7}$代入③得,y=-3×$\frac{4k-3}{7}$+2k=$\frac{2k+9}{7}$,
所以,方程组的解是$\left\{\begin{array}{l}{x=\frac{4k-3}{7}}\\{y=\frac{2k+9}{7}}\end{array}\right.$,
∵x<1且y>1,
∴$\left\{\begin{array}{l}{\frac{4k-3}{7}<1①}\\{\frac{2k+9}{7}>1②}\end{array}\right.$,
解不等式①得,k<$\frac{5}{2}$,
解不等式②得,k>1,
所以,不等式组的解集是1<k<$\frac{5}{2}$,
所以,k的整数解是k=2.
点评 本题考查的是二元一次方程组的解法,方程组中未知数的系数较小时可用代入法,当未知数的系数相等或互为相反数时用加减消元法较简单;一元一次不等式组解集的求法,其简便求法就是用口诀求解.求不等式组解集的口诀:同大取大,同小取小,大小小大中间找,大大小小找不到(无解);本题难点在于用k表示出x、y.


 课时训练江苏人民出版社系列答案
课时训练江苏人民出版社系列答案 黄冈经典趣味课堂系列答案
黄冈经典趣味课堂系列答案 启东小题作业本系列答案
启东小题作业本系列答案科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
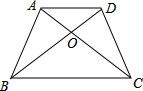 如图,梯形ABCD中,AD∥BC,对角线ACBD相交于点O,已知△AOD和△AOB的面积分别为2和4,则△ACD的面积为( )
如图,梯形ABCD中,AD∥BC,对角线ACBD相交于点O,已知△AOD和△AOB的面积分别为2和4,则△ACD的面积为( )| A. | 3 | B. | 4 | C. | 5 | D. | 6 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | x>-3 | B. | x<4 | C. | -3<x<4 | D. | -4<x<3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com