
 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案科目:初中数学 来源: 题型:解答题
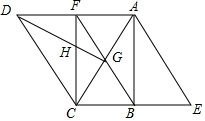 如图,在Rt△ABC中,∠ABC=90°,∠ACB=60°,将Rt△ABC绕点C逆时针旋转60°得到△DGC,点G在AC上,再将Rt△ABC沿着AB所在直线翻转180°得到△ABE,连接AD.
如图,在Rt△ABC中,∠ABC=90°,∠ACB=60°,将Rt△ABC绕点C逆时针旋转60°得到△DGC,点G在AC上,再将Rt△ABC沿着AB所在直线翻转180°得到△ABE,连接AD.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
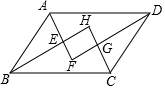 如图,在?ABCD中,AF、BH、CH、DF分别是∠DAB、∠ABC、∠BCD、∠CDA的平分线,AF与BH交于点E,CH与DF交于点G.在不添加其他条件的情况下,试写出上述条件推出的结论,并选择你喜欢的一个结论说明成立的理由.(要求推理过程中用到″平行四边形″和″角平分线″这两个条件).
如图,在?ABCD中,AF、BH、CH、DF分别是∠DAB、∠ABC、∠BCD、∠CDA的平分线,AF与BH交于点E,CH与DF交于点G.在不添加其他条件的情况下,试写出上述条件推出的结论,并选择你喜欢的一个结论说明成立的理由.(要求推理过程中用到″平行四边形″和″角平分线″这两个条件).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com