
【题目】如图,抛物线y=ax2+2x+c经过A(﹣1,0),B两点,且与y轴交于点C(0,3),抛物线与直线y=﹣x﹣1交于A,E两点.
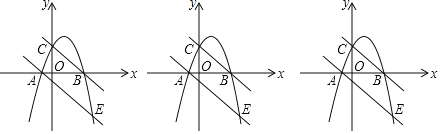
(1)求抛物线的解析式;
(2)坐标轴上是否存在一点Q,使得△AQE是以AE为底边的等腰三角形?若存在,请直接写出点Q的坐标;若不存在,说明理由.
(3)P点在x轴上且位于点B的左侧,若以P,B,C为顶点的三角形与△ABE相似,求点P的坐标.
【答案】(1)y=﹣x2+2x+3;(2)存在;Q1(4,0),Q2(0,﹣4);(3)(![]() ,0)或(﹣
,0)或(﹣![]() ,0).
,0).
【解析】
(1)将A、C的坐标代入y=ax2+2x+c求出a、c即可得到解析式;
(2)联立方程组求出E点坐标,分Q在x轴和y轴上两种情况讨论,分别根据QA2=QE2求出坐标即可;
(3)过点E作EH⊥x轴于点H,根据点E的坐标,分别求出AH=EH=5,AE=5![]() ,∠BAE=45°,以及OB=OC=3,∠ABC=45°,AB=4,BC=3
,∠BAE=45°,以及OB=OC=3,∠ABC=45°,AB=4,BC=3![]() ,所以只可能存在△PBC∽△BAE和△PBC∽△EAB两种情况,利用相似三角形对应边成比例即可求得点P的坐标.
,所以只可能存在△PBC∽△BAE和△PBC∽△EAB两种情况,利用相似三角形对应边成比例即可求得点P的坐标.
解:(1)将A(﹣1,0),C(0,3)代入y=ax2+2x+c,
得![]() ,
,
解得,![]() ,
,
∴抛物线的解析式为:y=﹣x2+2x+3,
故答案为:y=﹣x2+2x+3.
(2)存在.
联立 ,
,
解得,![]() 或
或![]() ,
,
∴E(4,﹣5),
如图1,当点Q在x轴上时,设Q(m,0),
∵AE为底边,
∴QA=QE,
∴QA2=QE2,
即(m+1)2=52+(m﹣4)2,
解得,m=4,
∴Q1(4,0);
当点Q在y轴上时,设Q(0,n),
∵AE为底边,
∴QA=QE,
∴QA2=QE2,
即n2+12=42+(n+5)2,
解得,n=﹣4,
∴Q2(0,﹣4),
综上所述,Q1(4,0),Q2(0,﹣4),
故答案为:存在;Q1(4,0),Q2(0,﹣4)

(3)如图2,过点E作EH⊥x轴于点H,
∵A(﹣1,0),E(4,﹣5),
∴AH=EH=5,AE=![]() =5
=5![]() ,∠BAE=45°,
,∠BAE=45°,
又OB=OC=3,
∴∠ABC=45°,AB=4,BC=![]() =3
=3![]() ,
,
设P(t,0),则BP=3﹣t,
∵∠BAE=∠ABC=45°,
∴只可能存在△PBC∽△BAE和△PBC∽△EAB两种情况,
当△PBC∽△BAE时,![]() ,
,
∴![]() =
=![]() ,
,
∴t=![]() ,
,
∴P1(![]() ,0);
,0);
当△PBC∽△EAB时,![]() ,
,
∴![]() =
=![]() ,
,
∴t=﹣![]() ,
,
∴P2(﹣![]() ,0),
,0),
综上所述,点P的坐标为(![]() ,0)或(﹣
,0)或(﹣![]() ,0),
,0),
故答案为:(![]() ,0)或(﹣
,0)或(﹣![]() ,0).
,0).


 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案 期末好成绩系列答案
期末好成绩系列答案科目:初中数学 来源: 题型:
【题目】如图,⊙O是△ABC的外接圆,AB为直径, OD∥BC交⊙O于点D,交AC于点E,连接AD,BD,CD.
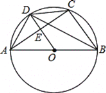
(1)求证:AD=CD;
(2)若AB=10,cos∠ABC=![]() ,求tan∠DBC的值.
,求tan∠DBC的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
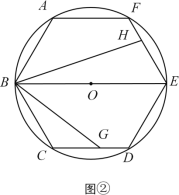
【题目】如图,已知圆O是正六边形ABCDEF外接圆,直径BE=8,点G、H分别在射线CD、EF上(点G不与点C、D重合),且∠GBH=60°,设CG=x,EH=y.
(1)如图①,当直线BG经过弧CD的中点Q时,求∠CBG的度数;
(2)如图②,当点G在边CD上时,试写出y关于x的函数关系式,并写出x的取值范围;
(3)联结AH、EG,如果△AFH与△DEG相似,求CG的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“互联网+”时代,网上购物备受消费者青睐,某网店专售一款休闲裤,其成本为每条40元,当售价为每条80元时,每月可售价100条.为了吸引更多顾客,该网店采取降价措施.据市场调查反映:销售单价每降![]() 元,则每月可多销售5条.设每条裤子的售价为
元,则每月可多销售5条.设每条裤子的售价为![]() 元(
元(![]() 为正整数),每月的销售量为
为正整数),每月的销售量为![]() 条.
条.
(1)直接写出![]() 与
与![]() 的函数关系式;
的函数关系式;
(2)设该网店每月获得的利润为![]() 元,当销售单价为多少元时,每月获得的利润最大,最大利润是多少?
元,当销售单价为多少元时,每月获得的利润最大,最大利润是多少?
(3)该网店店主热心公益事业,决定每月从利润中捐出200元资助贫困学生,为了保证捐款后每月利润不低于3800元,且让消费者得到最大的实惠,该如何确定休闲裤的销售单价?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,直线![]() 交
交![]() 轴于点
轴于点![]() ,交
,交![]() 轴于
轴于![]() ,抛物线
,抛物线![]() 经过点
经过点![]() 、
、![]() ,且与
,且与![]() 轴交于另一点
轴交于另一点![]() .
.
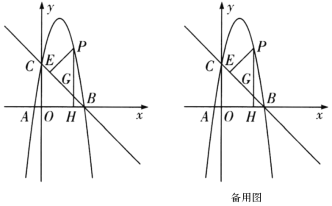
(1)求抛物线的解析式;
(2)点![]() 为第一象限内抛物线上一动点,过点
为第一象限内抛物线上一动点,过点![]() 作
作![]() 轴于点
轴于点![]() ,交直线
,交直线![]() 于点
于点![]() ,设点
,设点![]() 的横坐标为
的横坐标为![]() .
.
①过点![]() 作
作![]() 于点
于点![]() ,设
,设![]() 的长度为
的长度为![]() ,请用含
,请用含![]() 的式子表示
的式子表示![]() ,并求出当
,并求出当![]() 取得最大值时,点
取得最大值时,点![]() 的坐标.
的坐标.
②在①的条件下,当直线![]() 到直线
到直线![]() 的距离等于
的距离等于![]() 时,请直接写出符合要求的直线
时,请直接写出符合要求的直线![]() 的解析式.
的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(问题)用n个2×1矩形,镶嵌一个2×n矩形,有多少种不同的镶嵌方案?(2×n矩形表示矩形的邻边是2和n)
(探究)不妨假设有an种不同的镶嵌方案.为探究an的变化规律,我们采取一般问题特殊化的策略,先从最简单情形入手,再逐次递进,最后猜想得出结论.
探究一:用1个2×1矩形,镶嵌一个2×1矩形,有多少种不同的镶嵌方案?
如图(1),显然只有1种镶嵌方案.所以,a1=1.
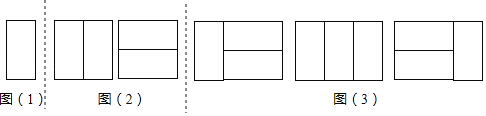
探究二:用2个2×1矩形,镶嵌一个2×2矩形,有多少种不同的镶嵌方案?
如图(2),显然只有2种镶嵌方案.所以,a2=2.
探究三:用3个2×1矩形,镶嵌一个2×3矩形,有多少种不同的镶嵌方案?
一类:在探究一每个镶嵌图的右侧再横着镶嵌2个2×1矩形,有1种镶嵌方案;
二类:在探究二每个镶嵌图的右侧再竖着镶嵌1个2×1矩形,有2种镶嵌方案;
如图(3).所以,a3=1+2=3.
探究四:用4个2×1矩形,镶嵌一个2×4矩形,有多少种不同的镶嵌方案?
一类:在探究二每个镶嵌图的右侧再横着镶嵌2个2×1矩形,有 种镶嵌方案;
二类:在探究三每个镶嵌图的右侧再竖着镶嵌1个2×1矩形,有 种镶嵌方案;
所以,a4= .
探究五:用5个2×1矩形,镶嵌一个2×5矩形,有多少种不同的镶嵌方案?
(仿照上述方法,写出探究过程,不用画图)
……
(结论)用n个2×1矩形,镶嵌一个2×n矩形,有多少种不同的镶嵌方案?
(直接写出an与an﹣1,an﹣2的关系式,不写解答过程).
(应用)用10个2×1矩形,镶嵌一个2×10矩形,有 种不同的镶嵌方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在![]() 中,
中,![]() ,
,![]() ,
,![]() ,点
,点![]() 由点
由点![]() 出发沿
出发沿![]() 方向向点
方向向点![]() 匀速运动,同时点
匀速运动,同时点![]() 由点
由点![]() 出发沿
出发沿![]() 方向向点
方向向点![]() 匀速运动,它们的速度均为
匀速运动,它们的速度均为![]() .连接
.连接![]() ,设运动时间为
,设运动时间为![]() .
.
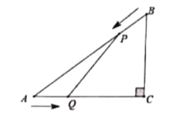
(1)当![]() 为何值时,
为何值时,![]() ?
?
(2)设![]() 的面积为
的面积为![]() ,求
,求![]() 与
与![]() 的函数关系式,并求出当
的函数关系式,并求出当![]() 为何值时,
为何值时,![]() 取得最大值?
取得最大值?![]() 的最大值是多少?
的最大值是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】据交管部门统计,高速公路超速行驶是引发交通事故的主要原因.我县某校数学课外小组的几个同学想尝试用自己所学的知识检测车速,渝黔高速公路某路段的限速是:每小时80千米(即最高时速不超过80千米),如图,他们将观测点设在到公路l的距离为0.1千米的P处.这时,一辆轿车由綦江向重庆匀速直线驶来,测得此车从A处行驶到B处所用的时间为3秒(注:3秒=![]() 小时),并测得∠APO=59°,∠BPO=45°.试计算AB并判断此车是否超速?(精确到0.001).(参考数据:sin59°≈0.8572,cos59°≈0.5150,tan59°≈1.6643)
小时),并测得∠APO=59°,∠BPO=45°.试计算AB并判断此车是否超速?(精确到0.001).(参考数据:sin59°≈0.8572,cos59°≈0.5150,tan59°≈1.6643)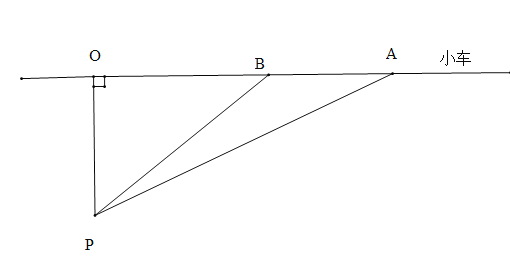
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com