
 已知:如图,在等腰三角形ABC中,AB=AC,P是底边BC上任意一点,过点P作PE⊥AB,PF⊥AC,垂足分别为E,F,过点B作BD⊥AC,垂足为D.求证:PE+PF=BD.
已知:如图,在等腰三角形ABC中,AB=AC,P是底边BC上任意一点,过点P作PE⊥AB,PF⊥AC,垂足分别为E,F,过点B作BD⊥AC,垂足为D.求证:PE+PF=BD.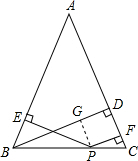 证明:过P作PG⊥BD于G,
证明:过P作PG⊥BD于G,
|


 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案 英才计划同步课时高效训练系列答案
英才计划同步课时高效训练系列答案科目:初中数学 来源: 题型:
 O的对称点,连接AC交x轴于点D,点A的坐标为(0,-3),sinB=
O的对称点,连接AC交x轴于点D,点A的坐标为(0,-3),sinB=| 3 | 5 |
查看答案和解析>>
科目:初中数学 来源: 题型:
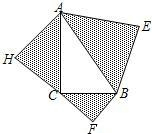 已知:如图,在Rt△ABC中,∠C=90°,以三角形的三边为斜边分别向外作等腰直角三角形,图中的三个等腰直角三角形的面积之和为50cm2,则AB=
已知:如图,在Rt△ABC中,∠C=90°,以三角形的三边为斜边分别向外作等腰直角三角形,图中的三个等腰直角三角形的面积之和为50cm2,则AB=查看答案和解析>>
科目:初中数学 来源: 题型:
 (2012•朝阳)已知,如图,在平面直角坐标系中,Rt△ABC的斜边BC在x轴上,直角顶点A在y轴的正半轴上,A(0,2),B(-1,0).
(2012•朝阳)已知,如图,在平面直角坐标系中,Rt△ABC的斜边BC在x轴上,直角顶点A在y轴的正半轴上,A(0,2),B(-1,0).查看答案和解析>>
科目:初中数学 来源: 题型:
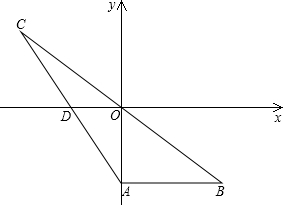
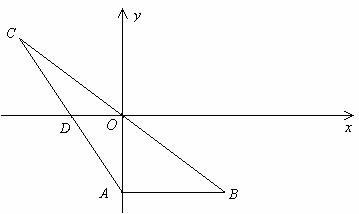
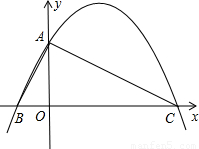
已知:如图,在平面直角坐标系![]() 中,
中,![]() ∥x轴,点C是点B关于原点O的对称点,连接AC交x轴于点D,点A的坐标为(0,-3),
∥x轴,点C是点B关于原点O的对称点,连接AC交x轴于点D,点A的坐标为(0,-3),![]() .
.
(1)求B、C、D三点的坐标;
(2)求过A、B、C三点的抛物线的解析式;
(3)设点E(8,n)在(2)中的抛物线上,请你在x轴上求一点F,使得
△DEF是以DE为底边的等腰三角形.
查看答案和解析>>
科目:初中数学 来源:2013年湖北省随州市中考数学模拟试卷(二)(解析版) 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com