
【题目】如图,已知点A的坐标为( ![]() ,3),AB丄x轴,垂足为B,连接OA,反比例函数y=
,3),AB丄x轴,垂足为B,连接OA,反比例函数y= ![]() (k>0)的图象与线段OA、AB分别交于点C、D.若AB=3BD,以点C为圆心,CA的
(k>0)的图象与线段OA、AB分别交于点C、D.若AB=3BD,以点C为圆心,CA的 ![]() 倍的长为半径作圆,则该圆与x轴的位置关系是(填”相离”,“相切”或“相交“).
倍的长为半径作圆,则该圆与x轴的位置关系是(填”相离”,“相切”或“相交“). 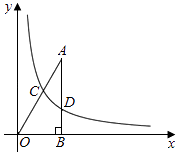
【答案】相交
【解析】解:∵已知点A的坐标为( ![]() ,3),AB=3BD, ∴AB=3,BD=1,
,3),AB=3BD, ∴AB=3,BD=1,
∴D点的坐标为( ![]() ,1),
,1),
∴反比例函数y= ![]() 解析式为:
解析式为:
y= ![]() ,
,
∴AO直线解析式为:y=kx,
3= ![]() k,
k,
∴k= ![]() ,
,
∴y= ![]() x,
x,
∴直线y= ![]() x与反比例函数y=
x与反比例函数y= ![]() 的交点坐标为:
的交点坐标为:
x=±1,
∴C点的横坐标为1,
纵坐标为: ![]() ,
,
过C点做CE垂直于OB于点E,
则CO=2,
∴AC=2 ![]() ﹣2,
﹣2,
∴CA的 ![]() 倍=
倍= ![]() ,
,
CE= ![]() ,
,
∵ ![]() ﹣
﹣ ![]() =
= ![]() ﹣
﹣ ![]() >0,
>0,
∴该圆与x轴的位置关系是相交.
所以答案是:相交.
【考点精析】本题主要考查了直线与圆的三种位置关系的相关知识点,需要掌握直线与圆有三种位置关系:无公共点为相离;有两个公共点为相交,这条直线叫做圆的割线;圆与直线有唯一公共点为相切,这条直线叫做圆的切线,这个唯一的公共点叫做切点才能正确解答此题.


 优生乐园系列答案
优生乐园系列答案科目:初中数学 来源: 题型:
【题目】如图,为了测量某建筑物CD的高度,先在地面上用测角仪自A处测得建筑物顶部的仰角是30°,然后在水平地面上向建筑物前进了100m,此时自B处测得建筑物顶部的仰角是45°.已知测角仪的高度是1.5m,请你计算出该建筑物的高度.(取 ![]() =1.732,结果精确到1m)
=1.732,结果精确到1m)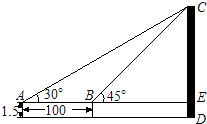
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一只不透明的袋子中装有2个白球和1个红球,这些球除颜色外其余都相同,搅匀后从中任意摸出1个球,记录下颜色后放回袋中并搅匀,再从中任意摸出1个球.请用画树状图的方法列出所有可能的结果,并写出两次摸出的球颜色相同的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算下列各式.
(1)(﹣2)3﹣|2﹣5|﹣(﹣15)
(2)﹣4![]() ﹣(+
﹣(+![]() )+(﹣5
)+(﹣5![]() )﹣(﹣
)﹣(﹣![]() )
)
(3)(﹣![]() +
+![]() ﹣
﹣![]() +
+![]() )÷(﹣
)÷(﹣![]() )
)
(4)18+32÷(﹣2)3﹣(﹣4)2×5
(5)﹣32﹣[(1![]() )3×(﹣
)3×(﹣![]() )﹣6÷|﹣
)﹣6÷|﹣![]() |]
|]
(6)2×(﹣1![]() )﹣2
)﹣2![]() ×13+(﹣1
×13+(﹣1![]() )×5+
)×5+![]() ×(﹣13)
×(﹣13)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,小明在大楼30米高(即PH=30米)的窗口P处进行观测,测得山坡上A处的俯角为15°,山脚B处的俯角为60°,巳知该山坡的坡度i(即tan∠ABC)为1: ![]() ,点P,H,B,C,A在同一个平面上,点H、B、C在同一条直线上,且PH丄HC.
,点P,H,B,C,A在同一个平面上,点H、B、C在同一条直线上,且PH丄HC.
(1)山坡坡角(即∠ABC)的度数等于度;
(2)求A、B两点间的距离(结果精确到0.1米,参考数据: ![]() ≈1.732).
≈1.732).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】光明中学十分重视中学生的用眼卫生,并定期进行视力检测.某次检测设有A、B两处检测点,甲、乙、丙三名学生各自随机选择其中的一处检测视力.
(1)求甲、乙、丙三名学生在同一处检测视力的概率;
(2)求甲、乙、丙三名学生中至少有两人在B处检测视力的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将ABCD的边DC延长到点E,使CE=DC,连接AE,交BC于点F. 
(1)求证:△ABF≌△ECF;
(2)若∠AFC=2∠D,连接AC、BE,求证:四边形ABEC是矩形.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com