
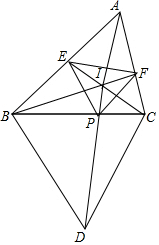
 如图,△ABC中,∠A=60°,以BC为边往外作等边△BCD,作∠B,∠C的角平分线分别交AC,AB于点F,E,若BE,CF交于点I,连接ID交BC于点P,求证:△EFP为等边三角形.
如图,△ABC中,∠A=60°,以BC为边往外作等边△BCD,作∠B,∠C的角平分线分别交AC,AB于点F,E,若BE,CF交于点I,连接ID交BC于点P,求证:△EFP为等边三角形. 分析 先根据角平分线和∠A=60°得:∠IBC+∠ICB=60°,证明I、B、D、C四点共圆,则∠BID=∠BCD=60°,∠DIC=∠DBC=60°,再证明△BEI≌△BPI,则EI=PI,同理可得:PI=FI,根据等边对等角可得:∠EPF=∠PFE=∠FEP=60°,所以△EFP是等边三角形.
解答  证明:∵∠A=60°,
证明:∵∠A=60°,
∴∠ABC+∠ACB=180°-60°=120°,
∵∠B,∠C的角平分线分别交AC,AB于点F,E,
∴∠IBC=$\frac{1}{2}$∠ABC,∠ICB=$\frac{1}{2}$∠ACB,
∴∠IBC+∠ICB=$\frac{1}{2}$(∠ABC+∠ACB)=$\frac{1}{2}$×120°=60°,
∴∠BIC=180°-60°=120°,∠EIB=60°,
∵△BCD是等边三角形,
∴∠BDC=60°,
∴∠BIC+∠BDC=120°+60°=180°,
∴I、B、D、C四点共圆,
∴∠BID=∠BCD=60°,
∠DIC=∠DBC=60°,
在△BEI和△BPI中,
∵$\left\{\begin{array}{l}{∠EBI=∠IBC}\\{BI=BI}\\{∠EIB=∠BIP=60°}\end{array}\right.$,
∴△BEI≌△BPI(ASA),
∴EI=PI,
同理可得:PI=FI,
∵∠EIF=120°,EI=FI,
∴∠IEF=∠IFE=30°,
同理得:∠IEP=∠IPE=30°,
∠IFP=∠IPF=30°,
∴∠EPF=∠PFE=∠FEP=60°,
∴△EFP是等边三角形.
点评 本题考查了四点共圆的判定和性质、三角形全等的性质和判定、等边三角形的性质和判定,熟练掌握四点共圆的判定是本题的关键,此题有难度.


科目:初中数学 来源: 题型:选择题
| A. | 22 | B. | 23 | C. | 24 | D. | 25 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 4 | B. | 5 | C. | 3 | D. | 6 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
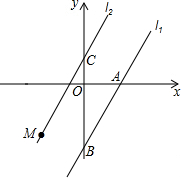 如图,一次函数l1:y=2x+b的图象与x轴、y轴分别相交于A、B两点,A的坐标为(2,0),y轴正半轴上有一点C(0,$\frac{3}{2}$),过点C有一条直线l2∥l1(l2与l1的k相等,即k2=k1),M是l2上任意一点.
如图,一次函数l1:y=2x+b的图象与x轴、y轴分别相交于A、B两点,A的坐标为(2,0),y轴正半轴上有一点C(0,$\frac{3}{2}$),过点C有一条直线l2∥l1(l2与l1的k相等,即k2=k1),M是l2上任意一点.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com