
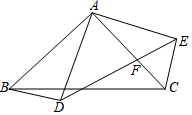
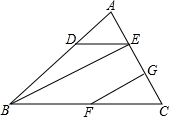
 如图△ABC与△ADE都是以A为直角顶点的等腰直角三角形,DE交AC于点F.
如图△ABC与△ADE都是以A为直角顶点的等腰直角三角形,DE交AC于点F.分析 (1)证明△BAD≌△CAE(SAS),可得BD=CE,根据角的关系可计算∠GBC+∠BCG=90°,从而得BD⊥CE;
(2)根据平行线的判定证明AB∥DE,得AD⊥BC,求BG和DG的长,利用勾股定理得BD的长.
解答 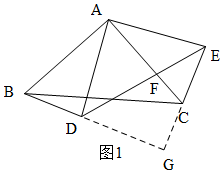 解:(1)BD=CE,且BD⊥CE,理由是:
解:(1)BD=CE,且BD⊥CE,理由是:
如图1,延长BD与EC交于点G,
∵△ABC与△ADE都是以A为直角顶点的等腰直角三角形,
∴AB=AC,AD=AE,∠BAC=∠DAE=90°,
∴∠BAC-∠DAC=∠DAE-∠DAC,
即∠BAD=∠CAE,
在△BAD和△CAE中,
∵$\left\{\begin{array}{l}{AB=AC}\\{∠BAD=∠CAE}\\{AD=AC}\end{array}\right.$,
∴△BAD≌△CAE(SAS),
∴BD=CE,∠ABD=∠ACE,
∴∠GBC+∠BCG=∠ABD-45°+180°-45°-∠ACE=90°,
∴∠G=90°,
∴BG⊥EG,
即BD⊥CE;
综上所述,BD=CE,且BD⊥CE;
(2)如图2,当∠CFE=90°时,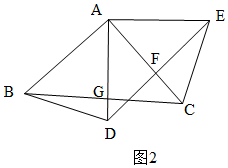
∵∠BAC=90°,
∴∠BAC=∠CFE,
∴AB∥DE,
∴∠BAD=∠ADE=45°,
∴AD平分∠BAC,
∴AD⊥BC,
∴△ABG是等腰直角三角形,
∵AB=10,
∴AG=BG=5$\sqrt{2}$,
∴DG=AD-AG=6$\sqrt{2}$-5$\sqrt{2}$=$\sqrt{2}$,
在Rt△BDG中,由勾股定理得:BD=$\sqrt{B{G}^{2}+D{G}^{2}}$=$\sqrt{(5\sqrt{2})^{2}+(\sqrt{2})^{2}}$=2$\sqrt{13}$.
点评 本题考查了等腰直角三角形的性质和判定、三角形全等的性质和判定、勾股定理,熟练掌握三角形全等的判定是关键.


 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案科目:初中数学 来源: 题型:填空题
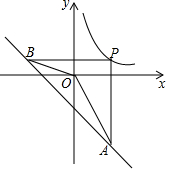 如图,P为反比例函数y=$\frac{k}{x}$(x>0)在第一象限内图象上的一点,过点P分别作x轴、y轴的垂线交一次函数y=-x-2的图象于点A、B.若AO、BO分别平分∠BAP、∠ABP,则k的值为2.
如图,P为反比例函数y=$\frac{k}{x}$(x>0)在第一象限内图象上的一点,过点P分别作x轴、y轴的垂线交一次函数y=-x-2的图象于点A、B.若AO、BO分别平分∠BAP、∠ABP,则k的值为2.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 随意掷一枚均匀的硬币两次,至少有一次反面朝上 | |
| B. | 今年冬天黑龙江会下雪 | |
| C. | 随意掷一枚均匀的正方体骰子两次,两次朝上面的点数之和为1 | |
| D. | 一个转盘被分成6个扇形,按红、白、白、红、红、白排列,转动转盘,指针停在红色区域 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 完成下面的证明:
完成下面的证明:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com