
【题目】如图,在△ABC中,AB=AC,AD平分∠BAC交BC于点D,分别过点A,D作AE∥BC,DE∥AB,AE与DE相交于点E,连结CE. 
(1)求证:AE=BD;
(2)求证:四边形ADCE是矩形.
【答案】
(1)证明:∵AE∥BC、DE∥AB,
∴四边形ABDE是平行四边形.
∴AE=BD
(2)证明:由(1)得:AE=BD,
∵AB=AC,AD平分∠BAC,
∴BD=CD,AD⊥BC,
∴AE=CD,∠ADC=90°,
又∵AE∥BC,
∴四边形ADCE是平行四边形.
∴四边形ADCE是矩形
【解析】(1)先证明四边形ABDE是平行四边形,得出AE=BD即可;(2)由等腰三角形的性质得出BD=CD,AD⊥BC,得出AE=CD,∠ADC=90°,证出四边形ADCE是平行四边形.即可得出结论.
【考点精析】本题主要考查了平行线的性质和等腰三角形的性质的相关知识点,需要掌握两直线平行,同位角相等;两直线平行,内错角相等;两直线平行,同旁内角互补;等腰三角形的两个底角相等(简称:等边对等角)才能正确解答此题.


科目:初中数学 来源: 题型:
【题目】如图,在梯形ABCD 中,AD∥BC,∠B=90°,AD=16cm,AB=12cm,BC=21cm,动点P从点B出发,沿射线BC的方向以每秒2cm的速度运动,动点Q从点A出发,在线段AD上以每秒lcm的速度向点D运动,点P,Q分别从点B,A同时出发,当点Q运动到点D时,点P随之停止运动,设运动的时间为t(秒). 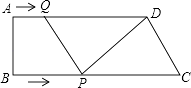
(1)当t为何值时,四边形PQDC是平行四边形.
(2)当t为何值时,以C、D、Q、P为顶点的梯形面积等于60cm2?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学校举行了主题为“让历史照亮未来”的演讲比赛,其中代表七、八年级参赛的两队各10人的比赛成绩如下表(10分制):
七年级队 | 7 | 8 | 9 | 7 | 10 | 10 | 9 | 10 | 10 | 10 |
八年级队 | 10 | 8 | 7 | 9 | 8 | 10 | 10 | 9 | 10 | 9 |
(1)请直接写出七年级队成绩的中位数为 , 八年级队成绩的众数为;
(2)若七、八年级队的平均成绩均为9分,请分别计算七、八年级队的方差.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场统计了每个营业员在某月的销售额,绘制了如下的条形统计图以及不完整的扇形统计图:
解答下列问题:
(1)设营业员的月销售额为x(单位:万元),商场规定:当x<15时为不称职,当15≤x<20时,为基本称职,当20≤x<25为称职,当x≥25时为优秀.则扇形统计图中的a= , b= .
(2)所有营业员月销售额的中位数和众数分别是多少?
(3)为了调动营业员的积极性,决定制定一个月销售额奖励标准,凡到达或超过这个标准的营业员将受到奖励.如果要使得营业员的半数左右能获奖,奖励标准应定为多少万元?并简述其理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com