
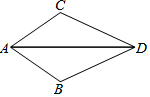
 如图,已知∠ADB=∠ADC,则不一定能使△ABD≌△ACD的条件是( )
如图,已知∠ADB=∠ADC,则不一定能使△ABD≌△ACD的条件是( )| A. | AB=AC | B. | BD=CD | C. | ∠B=∠C | D. | ∠BAD=∠CAD |
分析 利用全等三角形判定定理ASA,SAS,AAS对各个选项逐一分析即可得出答案.
解答 解:A、∵∠ADB=∠ADC,AD为公共边,若AB=AC,不符合全等三角形判定定理,不能判定△ABD≌△ACD;
B、∵∠ADB=∠ADC,AD为公共边,若BD=CD,则△ABD≌△ACD(SAS);
C、∵∠ADB=∠ADC,AD为公共边,若∠B=∠C,则△ABD≌△ACD(AAS);
D、∵∠ADB=∠ADC,AD为公共边,若∠BAD=∠CAD,则△ABD≌△ACD(ASA);
故选:A.
点评 本题考查三角形全等的判定方法,判定两个三角形全等的一般方法有:SSS、SAS、ASA、AAS、HL.注意:AAA、SSA不能判定两个三角形全等,判定两个三角形全等时,必须有边的参与,若有两边一角对应相等时,角必须是两边的夹角.


 全能测控一本好卷系列答案
全能测控一本好卷系列答案科目:初中数学 来源: 题型:解答题
 (1)观察思考
(1)观察思考查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,AB是斜靠在墙上的长梯,梯脚B距墙角1.4m,楼上点D距离墙1.2m,BD长0.5m,则梯子的长为( )
如图,AB是斜靠在墙上的长梯,梯脚B距墙角1.4m,楼上点D距离墙1.2m,BD长0.5m,则梯子的长为( )| A. | 3.2m | B. | 4m | C. | 3.5m | D. | 4.2m |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,在4×5的正方形网格中,已有线段AB,在格点中再取一点C,使△ABC成为等腰三角形,这样的点C有( )
如图,在4×5的正方形网格中,已有线段AB,在格点中再取一点C,使△ABC成为等腰三角形,这样的点C有( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,小明从A点出发前进10m,向右转15°,再前进10m,又向右转15°,…,这样一直走下去,他第一次回到出发点A时,一共走了( )
如图,小明从A点出发前进10m,向右转15°,再前进10m,又向右转15°,…,这样一直走下去,他第一次回到出发点A时,一共走了( )| A. | 240m | B. | 230m | C. | 220m | D. | 200m |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 有公共顶点的两个角是对顶角 | B. | 在一条直线上任取一点A | ||
| C. | 过点A作直线MN的垂线 | D. | 过点A作直线MN的平行线 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{{{({-3})}^2}}=3$ | B. | $\sqrt{3}×\sqrt{2}=\sqrt{6}$ | C. | $\sqrt{3}+\sqrt{2}=\sqrt{5}$ | D. | $\sqrt{6}÷\sqrt{3}=\sqrt{2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com