

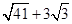 .
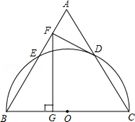
.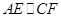 ,已知AE=4,CF=3,首先做出点A关于直径MN的对称点G点,可知点G也在圆上,连接对称点G和点C,那么与直径MN的交点,即为点P,那么也可以作点C关于直径的的对称点,同样也可以得到点P;(2)要求PA+PC的最短距离,根据(1)中的结论和题中条件如果点P在圆心,那么线段就是最短的,解决问题的关键在于题中AE=4,CF=3,再连接OA,OC,根据勾股定理和相似三角形的性质,即可得到线段相等,得到最短距离
,已知AE=4,CF=3,首先做出点A关于直径MN的对称点G点,可知点G也在圆上,连接对称点G和点C,那么与直径MN的交点,即为点P,那么也可以作点C关于直径的的对称点,同样也可以得到点P;(2)要求PA+PC的最短距离,根据(1)中的结论和题中条件如果点P在圆心,那么线段就是最短的,解决问题的关键在于题中AE=4,CF=3,再连接OA,OC,根据勾股定理和相似三角形的性质,即可得到线段相等,得到最短距离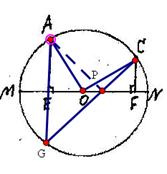
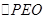 和
和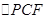 中,可到
中,可到
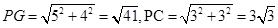
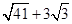


 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案科目:初中数学 来源:不详 题型:填空题
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:初中数学 来源:不详 题型:填空题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com