
【题目】如图,已知△ABC是面积为 ![]() 的等边三角形,△ABC∽△ADE,AB=2AD,∠BAD=45°,AC与DE相交于点F,则△AEF的面积等于(结果保留根号).
的等边三角形,△ABC∽△ADE,AB=2AD,∠BAD=45°,AC与DE相交于点F,则△AEF的面积等于(结果保留根号). 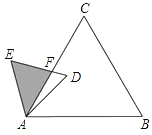
【答案】![]()
【解析】解:∵△ABC∽△ADE,AB=2AD, ∴ ![]() =
= ![]() ,
,
∵AB=2AD,S△ABC= ![]() ,
,
∴S△ADE= ![]() ,
,
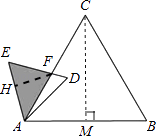
如图,在△EAF中,过点F作FH⊥AE交AE于H,
∵∠EAF=∠BAD=45°,∠AEF=60°,
∴∠AFH=45°,∠EFH=30°,
∴AH=HF,
设AH=HF=x,则EH=xtan30°= ![]() x.
x.
又∵S△ADE= ![]() ,
,
作CM⊥AB交AB于M,
∵△ABC是面积为 ![]() 的等边三角形,
的等边三角形,
∴ ![]() ×AB×CM=
×AB×CM= ![]() ,
,
∠BCM=30°,
设AB=2k,BM=k,CM= ![]() k,
k,
∴k=1,AB=2,
∴AE= ![]() AB=1,
AB=1,
∴x+ ![]() x=1,
x=1,
解得x= ![]() =
= ![]() .
.
∴S△AEF= ![]() ×1×
×1× ![]() =
= ![]() .
.
所以答案是: ![]() .
.
【考点精析】认真审题,首先需要了解等边三角形的性质(等边三角形的三个角都相等并且每个角都是60°),还要掌握相似三角形的性质(对应角相等,对应边成比例的两个三角形叫做相似三角形)的相关知识才是答题的关键.


 孟建平错题本系列答案
孟建平错题本系列答案 超能学典应用题题卡系列答案
超能学典应用题题卡系列答案科目:初中数学 来源: 题型:
【题目】如图,∠BAC的平分线交△ABC的外接圆于点D,∠ABC的平分线交AD于点E, 
(1)求证:DE=DB;
(2)若∠BAC=90°,BD=4,求△ABC外接圆的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】探索平方差公式的几何背景
如图1,边长为a的大正方形中有一个边长为b的小正方形.
(1)请表示图中阴影部分的面积: ;
(2)小颖将阴影部分拼成了一个长方形(如图2),这个长方形的长和宽分别是 ,它的面积是 ;

(3)比较(1)(2)的结果,你能验证平方差公式吗?说一说验证的理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ABC=∠ACB。

(1)若D为BC边上一点,E为直线AC上一点,且∠ADE=∠AED.求证:∠BAD=2∠CDE;
(2)如图,若D在BC的反向延长线上,其它条件不变,(1)中的结论是否仍然成立?证明你的结论.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ABC=90°,∠ACB=30°.将△ABC绕点A按逆时针方向旋转15°后得到△AB1C1 , B1C1交AC于点D,如果AD=2 ![]() ,则△ABC的周长等于 .
,则△ABC的周长等于 . 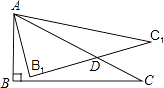
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学为了了解该校学生喜欢球类活动的情况,随机抽取了若干名学生进行问卷调查(要求每位学生只能填写一种自己喜欢的球类),并将调查的结果绘制成如下的两幅不完整的统计图,请根图中提供的信息,解答下列问题:
(1)参加调查的人数共有 人;
(2)将条形图补充完整;
(3)求在扇形图中表示“其它球类”的扇形的圆心角的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,直线AB分别交x、y轴于点A、B,直线BC分别交x、y轴于点C、B,点A的坐标为(3,0),∠ABO=30°,且AB⊥BC.
(1)求直线BC和AB的解析式;
(2)将点B沿某条直线折叠到点O,折痕分别交BC、BA于点E、D,在x轴上是否存在点F,使得点D、E、F为顶点的三角形是以DE为斜边的直角三角形?若存在,请求出F点坐标;若不存在,请说明理由;
(3)在平面直角坐标系内是否存在两个点,使得这两个点与B、C两点构成的四边形是正方形?若存在,请求出这两点的坐标;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,数轴上线段AB=2,CD=4,点A在数轴上表示的数是-10,点C在数轴上表示的数是16.若线段AB以6个单位长度/秒的速度向右匀速运动,同时线段CD以2个单位长度/秒的速度向左匀速运动.当B点运动到线段CD上时,P是线段AB上一点,且有关系式![]() =3成立,则线段PD的长为______________.
=3成立,则线段PD的长为______________.
![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com