练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    4．如图所示，课间操时，小华、小军、小刚的位置如图，小华对小刚说：“如果我的位置用（0，0）表示，小军的位置用（2，1）表示，那么你的位置应表示为（4，3）．”

    分析 根据小华的位置建立平面直角坐标系，进而得出答案．

    解答 解：如图所示：小刚的位置为：（4，3）．
    故答案为：（4，3）．

    点评 此题主要考查了坐标确定位置，正确建立平面直角坐标系是解题关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

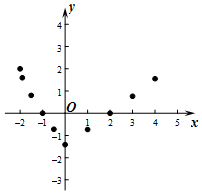    14．有这样一个问题：探究函数y=-$\sqrt{x+2}$+|x|的图象与性质．?
    小军根据学习函数的经验，对函数y=-$\sqrt{x+2}$+|x|的图象与性质进行了探究．
    下面是小军的探究过程，请补充完整：
    （1）函数y=-$\sqrt{x+2}$+|x|的自变量x的取值范围是x≥-2；
    （2）表是y与x的几组对应值?
    x-2-1.9-1.5-1-0.501234…
    y21.600.800-0.72-1.41-0.3700.761.55…
    在平面直角坐标系xOy中，描出了以上表中各对对应值为坐标的点，根据描出的点，画出该函数的图象；
    （3）观察图象，函数的最小值是-$\sqrt{2}$；
    （4）进一步探究，结合函数的图象，写出该函数的一条性质（函数最小值除外）：当-2≤x＜0时，y随x的增大而减小．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    15．如图，已知四边形ABCD是矩形，对角线AC、BD交于点O，CE∥BD，DE∥AC，CE与DE交于点E．
    求证：四边形OCED是菱形．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

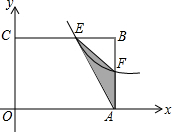    12．如图，在矩形OABC中，OA=3，OC=2，F是AB上的一个动点（F不与A，B重合），过点F的反比例函数y=$\frac{k}{x}$（k＞0）的图象与BC边交于点E．
    （1）当F为AB的中点时，求该函数的解析式；
    （2）当k为何值时，△EFA的面积为$\frac{2}{3}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    19．如图，△ABC中，BC=a，AC=b，AB=c（b＜c＜a），BC的垂直平分线DG交∠BAC的角平分线AD于点D，DE⊥AB于E，DF⊥AC于F，则下列结论一定成立的是（　　）
    A．DG=$\frac{1}{2}$（a+b）B．CF=c-bC．BE=$\frac{1}{2}$（a-b）D．AE=$\frac{1}{2}$（b+c）

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    9．计算：
    （1）$\sqrt{25}$-$\root{3}{27}$+$\sqrt{\frac{1}{4}}$；
    （2）$\sqrt{（-2）^{2}}$+|$\sqrt{2}$-1|-（$\sqrt{2}$+1）．
    （3）（-$\frac{1}{2}$）2+$\frac{3}{4}$-（2-$\sqrt{3}$）+|2-$\sqrt{3}$|

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

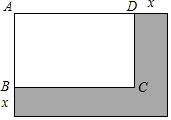    16．如图，矩形ABCD的长AD=5cm，宽AB=3cm，长和宽都增加xcm，那么面积增加ycm2．
    （1）写出y与x的函数关系式；
    （2）当增加的面积y=20cm2时，求相应的x是多少？

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    13．杨辉是我国南宋末年的一位杰出的数学家．在他著的《详解九章算法》一书中，画了一张表示二项式展开后的系数构成的三角图形，称做“开方做法本源”，现在简称为“杨辉三角”，它是杨辉的一大重要研究成果．
    我们把杨辉三角的每一行分别相加，如下：
    1               （  1  ）
    1   1             （ 1+1=2  ）
    1   2   1           （1+2+1=4  ）
    1   3   3   1         （1+3+3+1=8  ）
    1   4   6   4   1       （1+4+6+4+1=16  ）
    1   5  10  10   5  1      （1+5+10+10+5+1=32  ）
    1   6  15  20  15  6   1   （1+6+15+20+15+6+1=64  ）
    …写出杨辉三角第n行中n个数之和等于2n-1．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

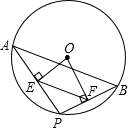    14．如图，点A、B是⊙O上两点，AB=10，点P是⊙O上的动点（P与A、B不重合），连结AP、PB，过点O分别作OE⊥AP于点E，OF⊥AP于点E，OF⊥PB于点F，则EF=（　　）
    A．4B．5C．5.5D．6

    查看答案和解析>>

    同步练习册答案