
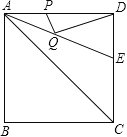
【题目】如图,正方形ABCD的边长是2,∠DAC的平分线交DC于点E,若点P、Q分别是AD和AE上的动点,则DQ+PQ的最小值为 .
【答案】![]() .
.
【解析】
试题过D作AE的垂线交AE于F,交AC于D′,再过D′作D′P′⊥AD,由角平分线的性质可得出D′是D关于AE的对称点,进而可知D′P′即为DQ+PQ的最小值.
作D关于AE的对称点D′,再过D′作D′P′⊥AD于P′,
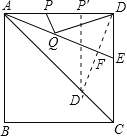
∵DD′⊥AE,
∴∠AFD=∠AFD′,
∵AF=AF,∠DAE=∠CAE,
∴△DAF≌△D′AF,
∴D′是D关于AE的对称点,AD′=AD=2,
∴D′P′即为DQ+PQ的最小值,
∵四边形ABCD是正方形,
∴∠DAD′=45°,
∴AP′=P′D′,
∴在Rt△AP′D′中,
P′D′2+AP′2=AD′2,AD′2=4,
∵AP′=P′D',
2P′D′2=AD′2,即2P′D′2=4,
∴P′D′=![]()
,即DQ+PQ的最小值为![]() .
.


科目:初中数学 来源: 题型:
【题目】在美化校园的活动中,某兴趣小组想借助如图所示的直角墙角(两边足够长),用28m长的篱笆围成一个矩形花园ABCD(篱笆只围AB、BC两边),设AB=xm.

(1)若花园的面积为192m2,求x的值;
(2)若在P处有一棵树与墙CD、AD的距离分别是13m和6m,要将这棵树围在花园内(含边界,不考虑树的粗细),求花园面积S的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】平面直角坐标系xOy中,对称轴平行于y轴的抛物线过点A(1,0)、B(3,0)和C(4,6);
(1)求抛物线的表达式;
(2)现将此抛物线先沿x轴方向向右平移6个单位,再沿y轴方向平移k个单位,若所得抛物线与x轴交于点D、E(点D在点E的左边),且使△ACD∽△AEC(顶点A、C、D依次对应顶点A、E、C),试求k的值,并注明方向.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】读一读:式子“1+2+3+4+5+…+100”表示1开始的100个连续自然数的和.由于上述式子比较长,书写也不方便,为了简便起见,我们可以将“1+2+3+4+5+…+100”表示为![]() ,这里“
,这里“![]() ”是求和符号.例如:1+3+5+7+9+…+99,即从1开始的100以内的连续奇数的和,可表示为
”是求和符号.例如:1+3+5+7+9+…+99,即从1开始的100以内的连续奇数的和,可表示为![]() (2n-1);又如13+23+33+43+53+63+73+83+93+103可表示为
(2n-1);又如13+23+33+43+53+63+73+83+93+103可表示为![]() n3.
n3.
通过对上以材料的阅读,请解答下列问题.
(1)2+4+6+8+10+…+100(即从2开始的100以内的连续偶数的和)用求和符合可表示为_________________;
(2)计算![]() (n2-1)=________________.(填写最后的计算结果)
(n2-1)=________________.(填写最后的计算结果)
查看答案和解析>>
科目:初中数学 来源: 题型:
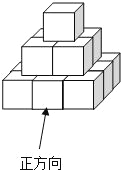
【题目】把棱长为1cm的若干个小正方体摆放如图所示的几何体,然后在露出的表面上涂上颜色![]() 不含底面
不含底面![]()
![]() 该几何体中有多少小正方体?
该几何体中有多少小正方体?
![]() 画出主视图.
画出主视图.
![]() 求出涂上颜色部分的总面积.
求出涂上颜色部分的总面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某工厂在生产过程中要消耗大量电能,消耗每千度电产生利润与电价是一次函数关系,经过测算,工厂每千度电产生利润y(元/千度))与电价x(元/千度)的函数图象如图:
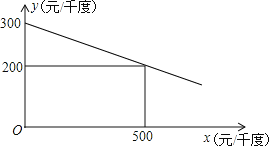
(1)当电价为600元/千度时,工厂消耗每千度电产生利润是多少?
(2)为了实现节能减排目标,有关部门规定,该厂电价x(元/千度)与每天用电量m(千度)的函数关系为x=10m+500,且该工厂每天用电量不超过60千度,为了获得最大利润,工厂每天应安排使用多少度电?工厂每天消耗电产生利润最大是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
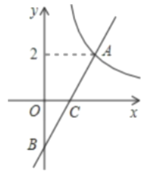
【题目】如图在平面直角坐标系![]() 中,函数
中,函数![]() 的图象与一次函数
的图象与一次函数![]() 的图象的交点为
的图象的交点为![]() .
.
(1)求一次函数的解析式;
(2)设一次函数![]() 的图象与
的图象与![]() 轴交于点
轴交于点![]() ,若点
,若点![]() 是
是![]() 轴上一点,且满足
轴上一点,且满足![]() 的面积是6,求点
的面积是6,求点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】气象台发布的卫星云图显示,代号为![]() 的台风在某海岛(设为点
的台风在某海岛(设为点![]() )的南偏东
)的南偏东![]() 方向的
方向的![]() 点生成,测得
点生成,测得![]() .台风中心从点
.台风中心从点![]() 以
以![]() 的速度向正北方向移动,经
的速度向正北方向移动,经![]() 后到达海面上的点
后到达海面上的点![]() 处.因受气旋影响,台风中心从点
处.因受气旋影响,台风中心从点![]() 开始以
开始以![]() 的速度向北偏西
的速度向北偏西![]() 方向继续移动.以
方向继续移动.以![]() 为原点建立如图所示的直角坐标系.
为原点建立如图所示的直角坐标系.
(1)台风中心生成点![]() 的坐标为 ,台风中心转折点
的坐标为 ,台风中心转折点![]() 的坐标为 ;(结果保留根号)
的坐标为 ;(结果保留根号)
(2)已知距台风中心![]() 范围内均会受到台风侵袭.如果某城市(设为点
范围内均会受到台风侵袭.如果某城市(设为点![]() )位于点
)位于点![]() 的正北方向且处于台风中心的移动路线上,那么台风从生成到最初侵袭该城要经过多长时间?
的正北方向且处于台风中心的移动路线上,那么台风从生成到最初侵袭该城要经过多长时间?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx+c的图象如图,则下列叙述正确的是( )

A. abc<0 B. -3a+c<0
C. b2-4ac≥0 D. 将该函数图象向左平移2个单位后所得到抛物线的解析式为y=ax2+c
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com