
【题目】如图,已知抛物线![]() 过点A(
过点A(![]() ,-3) 和B(3
,-3) 和B(3![]() ,0),过点A作直线AC//x轴,交y轴与点C.
,0),过点A作直线AC//x轴,交y轴与点C.
(1)求抛物线的解析式;
(2)在抛物线上取一点P,过点P作直线AC的垂线,垂足为D,连接OA,使得以A,D,P为顶点的三角形与△AOC相似,求出对应点P的坐标;
(3)抛物线上是否存在点Q,使得![]() ?若存在,求出点Q的坐标;若不存在,请说明理由.
?若存在,求出点Q的坐标;若不存在,请说明理由.
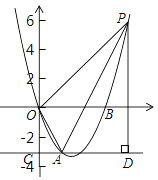
【答案】(1)![]() ;(2)P点坐标为(4
;(2)P点坐标为(4![]() ,6)或(
,6)或(![]() ,-
,- ![]() );(3)Q点坐标(3
);(3)Q点坐标(3![]() ,0)或(-2
,0)或(-2![]() ,15)
,15)
【解析】
(1)把A与B坐标代入抛物线解析式求出a与b的值,即可确定出解析式;
(2)设P坐标为![]() ,表示出AD与PD,由相似分两种情况得比例求出x的值,即可确定出P坐标;
,表示出AD与PD,由相似分两种情况得比例求出x的值,即可确定出P坐标;
(3)存在,求出已知三角形AOC边OA上的高h,过O作OM⊥OA,截取OM=h,与y轴交于点N,分别确定出M与N坐标,利用待定系数法求出直线MN解析式,与抛物线解析式联立求出Q坐标即可.
(1)把![]() ,
,![]() 和点
和点![]() ,
,![]() 代入抛物线得:
代入抛物线得:![]() ,
,
解得:![]() ,
,![]() ,
,
则抛物线解析式为![]() ;
;
(2)当![]() 在直线
在直线![]() 上方时,
上方时,
设![]() 坐标为
坐标为![]() ,则有
,则有![]() ,
,![]() ,
,
当![]() 时,
时,![]() ,即
,即![]() ,
,
整理得:![]() ,即
,即![]() ,
,
解得:![]() ,即
,即![]() 或
或![]() (舍去),
(舍去),
此时![]() ,
,![]() ;
;
当![]() 时,
时,![]() ,即
,即![]() ,
,
整理得:![]() ,即
,即![]() ,
,
解得:![]() ,即
,即![]() 或
或![]() (舍去),
(舍去),
此时![]() ,
,![]() ;
;
当点![]() 时,也满足
时,也满足![]() ;
;
当![]() 在直线
在直线![]() 下方时,同理可得:
下方时,同理可得:![]() 的坐标为
的坐标为![]() ,
,![]() ,
,
综上,![]() 的坐标为
的坐标为![]() ,
,![]() 或
或![]() ,
,![]() 或
或![]() ,
,![]() 或
或![]() ;
;
(3)在![]() 中,
中,![]() ,
,![]() ,
,
根据勾股定理得:![]() ,
,
![]()
![]() ,
,
![]() ,
,
![]() ,
,
![]() 边
边![]() 上的高为
上的高为![]() ,
,
过![]() 作
作![]() ,截取
,截取![]() ,过
,过![]() 作
作![]() ,交
,交![]() 轴于点
轴于点![]() ,如图所示:
,如图所示:
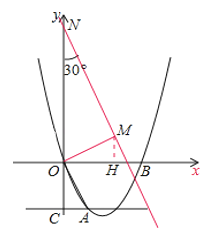
在![]() 中,
中,![]() ,即
,即![]() ,
,
过![]() 作
作![]() 轴,
轴,
在![]() 中,
中,![]() ,
,![]() ,即
,即![]() ,
,![]() ,
,
设直线![]() 解析式为
解析式为![]() ,
,
把![]() 坐标代入得:
坐标代入得:![]() ,即
,即![]() ,即
,即![]() ,
,
联立得: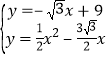 ,
,
解得:![]() 或
或![]() ,即
,即![]() ,
,![]() 或
或![]() ,
,![]() ,
,
则抛物线上存在点![]() ,使得
,使得![]() ,此时点
,此时点![]() 的坐标为
的坐标为![]() ,
,![]() 或
或![]() ,
,![]() .
.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
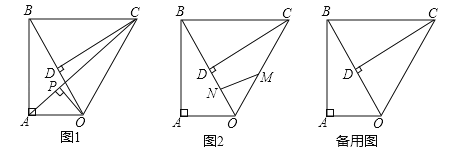
【题目】已知![]() ,
,![]() ,
,![]() ,斜边
,斜边![]() ,将
,将![]() 绕点
绕点![]() 顺时针旋转
顺时针旋转![]() ,如图1,连接
,如图1,连接![]() .
.
(1)填空:![]()
![]() ;
;
(2)如图1,连接![]() ,作
,作![]() ,垂足为
,垂足为![]() ,求
,求![]() 的长度;
的长度;
(3)如图2,点![]() ,
,![]() 同时从点
同时从点![]() 出发,在
出发,在![]() 边上运动,
边上运动,![]() 沿
沿![]() 路径匀速运动,
路径匀速运动,![]() 沿
沿![]() 路径匀速运动,当两点相遇时运动停止,已知点
路径匀速运动,当两点相遇时运动停止,已知点![]() 的运动速度为1.5单位
的运动速度为1.5单位![]() 秒,点
秒,点![]() 的运动速度为1单位
的运动速度为1单位![]() 秒,设运动时间为
秒,设运动时间为![]() 秒,
秒,![]() 的面积为
的面积为![]() ,求当
,求当![]() 为何值时
为何值时![]() 取得最大值?最大值为多少?
取得最大值?最大值为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线y=ax2-4x+c(a≠0)与反比例函数y=![]() 的图象相交于B点,且B点的横坐标为3,抛物线与y轴交于点C(0,6),A是抛物线y=ax2-4x+c的顶点,P点是x轴上一动点,当PA+PB最小时,P点的坐标为_______.
的图象相交于B点,且B点的横坐标为3,抛物线与y轴交于点C(0,6),A是抛物线y=ax2-4x+c的顶点,P点是x轴上一动点,当PA+PB最小时,P点的坐标为_______.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知,梯形![]() 中,
中,![]() ,
,![]() ,
,![]() ∥
∥![]() ,
,![]() ,
,![]() ,点
,点![]() 在
在![]() 边上,以点
边上,以点![]() 为圆心
为圆心![]() 为半径作弧交边
为半径作弧交边![]() 于点
于点![]() ,射线
,射线![]() 与射线
与射线![]() 交于点
交于点![]() .
.
(1)若![]() ,求
,求![]() 的长;
的长;
(2)联结![]() ,若
,若![]() ,求
,求![]() 的长;
的长;
(3)线段![]() 上是否存在点
上是否存在点![]() ,使得△
,使得△![]() 与△
与△![]() 相似,若相似,求
相似,若相似,求![]() 的值,若不相似,请说明理由
的值,若不相似,请说明理由
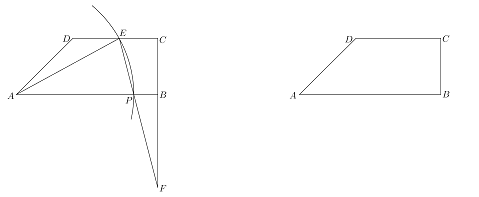
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有大小两种货车,3辆大货车与4辆小货车一次可以运货18吨,2辆大货车与6辆小货车一次可以运货17吨.
(1)请问1辆大货车和1辆小货车一次可以分别运货多少吨?
(2)目前有33吨货物需要运输,货运公司拟安排大小货车共计10辆,全部货物一次运完,其中每辆大货车一次运费花费130元,每辆小货车一次运货花费100元,请问货运公司应如何安排车辆最节省费用?
查看答案和解析>>
科目:初中数学 来源: 题型:
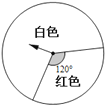
【题目】如图是一个可以自由转动的转盘,小明跟小红分别转动一次转盘,然后记下转盘停止时指针所指的颜色(指针压线时重转),若两次颜色相同则小明获胜,否则小红获胜,请你用树状图或列表的方法表示这个游戏所有可能出现的结果,并判断游戏是否公平.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(9分)九年级数学兴趣小组经过市场调查,得到某种运动服每月的销量与售价的相关信息如下表:
售价(元/件) | 100 | 110 | 120 | 130 | … |
月销量(件) | 200 | 180 | 160 | 140 | … |
已知该运动服的进价为每件60元,设售价为![]() 元.
元.
(1)请用含x的式子表示:①销售该运动服每件的利润是 元;②月销量是 件;(直接写出结果)
(2)设销售该运动服的月利润为![]() 元,那么售价为多少时,当月的利润最大,最大利润是多少?
元,那么售价为多少时,当月的利润最大,最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx+c的图象经过点A(-1,0),B(1,4),C(0,3).
(1)求出此二次函数的表达式,并把它化成![]() 的形式;
的形式;
(2)请在坐标系内画出这个函数的图象,并根据图象写出函数值y为负数时,自变量x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
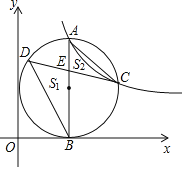
【题目】如图,点A是反比例函数![]() 图象第一象限上一点,过点A作
图象第一象限上一点,过点A作![]() 轴于B点,以AB为直径的圆恰好与y轴相切,交反比例函数图象于点C,在AB的左侧半圆上有一动点D,连结CD交AB于点
轴于B点,以AB为直径的圆恰好与y轴相切,交反比例函数图象于点C,在AB的左侧半圆上有一动点D,连结CD交AB于点![]() 记
记![]() 的面积为
的面积为![]() ,
,![]() 的面积为
的面积为![]() ,连接BC,则
,连接BC,则![]() 是______三角形,若
是______三角形,若![]() 的值最大为1,则k的值为______.
的值最大为1,则k的值为______.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com