
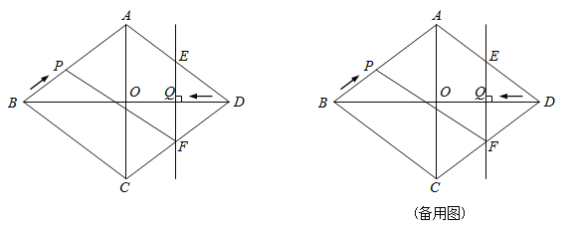
����Ŀ����֪����ͼ������ABCD�����Խ���AC��BD�ཻ�ڵ�O����AC��12cm��BD��16cm����P�ӵ�B��������BA���������˶����ٶ�Ϊ1cm/s��ͬʱ��ֱ��EF�ӵ�D��������DB���������˶����ٶ�Ϊ1cm/s��EF��BD������AD��BD��CD�ֱ��ڵ�E��Q��F����ֱ��EFֹͣ�˶�ʱ����PҲֹͣ�˶�������PF�����˶�ʱ��Ϊt��s����0��t��8�����������������
��1����tΪ��ֵʱ���ı���APFD��ƽ���ı�����
��2�����ı���APFE�����Ϊy��cm2������y��t֮��ĺ�����ϵʽ��
��3���Ƿ����ijһʱ��t��ʹS�ı���APFE��S����ABCD��17��40�������������t��ֵ���������ʱP��E�����ľ�����������������˵��������
���𰸡���1�� ��t=![]() sʱ���ı���APFD��ƽ���ı��Σ���2��y=-
sʱ���ı���APFD��ƽ���ı��Σ���2��y=-![]() t2+
t2+![]() t+48����3�� PE=
t+48����3�� PE=![]() ��cm����
��cm����
��������
���⣨1�������ı���ABCD�����Σ�OA=![]() AC��OB=
AC��OB=![]() BD����Rt��AOB�У����ù��ɶ������AB=10��������DFQ�ס�DCO���ó�
BD����Rt��AOB�У����ù��ɶ������AB=10��������DFQ�ס�DCO���ó�![]() �����DF����AP=DF�����t��
�����DF����AP=DF�����t��
��2������C��CG��AB�ڵ�G����S����ABCD=ABCG=![]() ACBD�����CG����S����APFD=
ACBD�����CG����S����APFD=![]() ��AP+DF��CG��S��EFD=
��AP+DF��CG��S��EFD=![]() EFQD���ó�y��t֮��ĺ�����ϵʽ��
EFQD���ó�y��t֮��ĺ�����ϵʽ��
��3������C��CG��AB�ڵ�G����S����ABCD=ABCG�����CG����S�ı���APFE��S����ABCD=17��40�����t��������PBN�ס�ABO�����PN��BN�����߶ι�ϵ���EM��PM���ɹ��ɶ������PE��
�����������1�����ı���ABCD�����Σ�
��AB��CD��AC��BD��OA=OC=![]() AC=6�� OB=OD=
AC=6�� OB=OD=![]() BD=8��
BD=8��
��Rt��AOB��AB=10
��EF��BD��
���FQD=��COD=90����
���ߡ�FDQ=��CDO��
���DFQ�ס�DCO��
��![]() ����
����![]()
��DF=![]()
���ı���APFD��ƽ���ı��Σ�
��AP=DF��
��10-t=![]()
��������̣���t=![]() ��
��
����t=![]() sʱ���ı���APFD��ƽ���ı��Σ�
sʱ���ı���APFD��ƽ���ı��Σ�
��2����ͼ������C��CG��AB�ڵ�G��
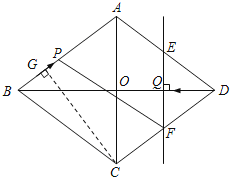
��S����ABCD=ABCG=![]() ACBD��
ACBD��
��10CG=![]() ��12��16��
��12��16��
��CG=![]()
��S����APFD=![]() ��AP+DF��CG
��AP+DF��CG
=![]() ��10-t+
��10-t+![]() ��
��![]()
=![]() t+48��
t+48��
�ߡ�DFQ�ס�DCO��
��![]()
��![]()
��QF=![]() ��
��
ͬ����EQ=![]()
��EF=QF+EQ=![]() ��
��
��S��EFD=![]() EFQD=
EFQD=![]() ��
��![]() ��t=
��t=![]() ��
��
��y=��![]() t+48��-
t+48��-![]() =-
=-![]() +
+![]() t+48��
t+48��
��3����ͼ������P��PM��EF�ڵ�M��PN��BD�ڵ�N��

��S�ı���APFE��S����ABCD=17��40��
��-![]() +
+![]() t+48=
t+48=![]() ��96��
��96��
��5t2-8t-48=0��
��������̣���t1=4��t2=-![]() ����ȥ��
����ȥ��
����P��PM��EF�ڵ�M��PN��BD�ڵ�N��
��t=4ʱ��
�ߡ�PBN�ס�ABO��
��![]()
��![]()
��PN=![]() ��BN=
��BN=![]()
��EM=EQ-MQ=3-![]() =
=![]()
PM=BD-BN-DQ=16-![]() -4=
-4=![]()
��Rt��PME��
PE=![]() cm.
cm.


 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
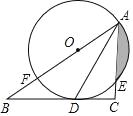
����Ŀ����ͼ����Rt��ABC�У�![]() ��ADƽ�֡�BAC����BC�ڵ�D����O��AB�ϣ���O����A��D���㣬��AC�ڵ�E����AB�ڵ�F��
��ADƽ�֡�BAC����BC�ڵ�D����O��AB�ϣ���O����A��D���㣬��AC�ڵ�E����AB�ڵ�F��
��1����֤��BC�ǡ�O�����ߣ�
��2������O�İ뾶��2cm��E�ǻ�AD���е㣬����Ӱ���ֵ��������������к��ţ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
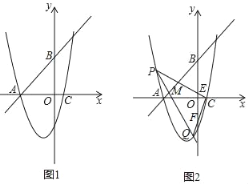
����Ŀ����ͼ1��������y=��x2+mx+n��x���ڵ�A����2��0���͵�B����y���ڵ�C��0��2����
��1���������ߵĺ�������ʽ��
��2������M���������ϣ���S��AOM=2S��BOC�����M�����ꣻ
��3����ͼ2�����N���߶�AC�ϵ�һ���㣬��DN��x�ᣬ���������ڵ�D�����߶�DN���ȵ����ֵ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ֱ֪��y��x+4�ֱ�x�ᡢy����A��B���㣬������y��x2+mx��4������A����x�����һ������ΪC��
��1���������ߵĽ���ʽ��
��2����ͼ1����D���������ϵĶ��㣬���ڵ������ޣ����ABD��������ֵ��
��3����ͼ2��������M����4��1����ֱ�߽��������ڵ�P��Q������CP��CQ�ֱ�y���ڵ�E��F����OEOF��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
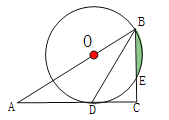
����Ŀ����ͼ����Rt��ABC������C=90�㣬BD�ǽ�ƽ��������O��AB�����Ե�OΪԲ����OBΪ�뾶��Բ������D����BC�ڵ�E��
��1����֤��AC����O��������
��2����OB=10��CD=![]() ����ͼ����Ӱ���ֵ������
����ͼ����Ӱ���ֵ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
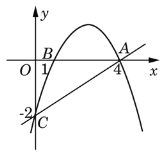
����Ŀ����ͼ�������߾���A(4��0)��B(1��0)��C(0����2)���㣮
(1)��������ߵĽ���ʽ��
(2)P����������һ���㣬��P��PM��x�ᣬ����ΪM���Ƿ����P�㣬ʹ����A��P��MΪ��������������OAC���ƣ������ڣ���������������ĵ�P�����ꣻ�������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����x�ķ���kx2+��2k��1��x+k��1��0��1��ֻ�����������ҹ���y��һԪ���η��̣�k��1��y2��3y+m��0��2��������ʵ����y1��y2
��1����kΪ����ʱ��ȷ��k��ֵ��
��2���ڣ�1���������£���m����2���ù���m�Ĵ���ʽ��ʾy12+y22��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
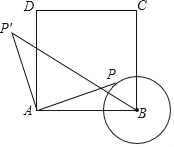
����Ŀ����ͼ��������ABCD�У�AB��3cm����BΪԲ�ģ�1cm��Ϊ�뾶����B����P�ڡ�B���ƶ�������AP������AP�Ƶ�A��ʱ����ת90����AP�䣬����BP�䣮�ڵ�P�ƶ��Ĺ����У�BP�䳤�ȵ���СֵΪ_____cm��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���������Ǻ��������µĹ�ʽ��
sin����+�£�=sin��cos��+cos��sin�¢�
cos����+�£�=cos��cos�©�sin��sin�¢�
tan����+�£�=![]() ��
��
������Щ��ʽ�ɽ�ijЩ��������ǵ����Ǻ���ת��Ϊ����ǵ����Ǻ�������ֵ���磺
tan105��=tan��45��+60�㣩=![]() =����2+
=����2+![]() ����
����
���������֪ʶ�������ѡ���ʵ��Ĺ�ʽ��������ʵ�����⣺
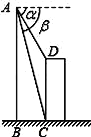
��ͼ��ֱ���ɻ���һ������CD�Ϸ�A�㴦��ý����ﶥ��D��ĸ��Ǧ�=60�㣬��C��ĸ��Ǧ�=75�㣬��ʱֱ���ɻ��뽨����CD��ˮƽ����BCΪ42m��������CD�ĸߣ�
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com