Question

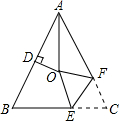
19．如图，△ABC中，AB=AC，∠BAC=50°，∠BAC的平分线与AB的垂直平分线交于点O，将∠C沿EF（E在BC上，F在AC上）折叠，点C与点O恰好重合，则∠OEC的度数是（　　）

• A． 100°
• B． 108°
• C． 120°
• D． 126°

Answer 1

分析 如图，作辅助线，首先求出∠BAO=25°；进而求出∠OBC=40°；求出∠COE=∠OCB=40°问题即可解决．

解答 解：∵∠BAC=50°，AO为∠BAC的平分线，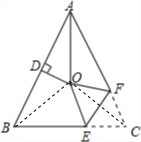
∴∠BAO=$\frac{1}{2}$∠BAC=$\frac{1}{2}$×50°=25°．
又∵AB=AC，
∴∠ABC=∠ACB=$\frac{180°-50°}{2}$．
∵DO是AB的垂直平分线，
∴OA=OB；
∴∠ABO=∠BAO=25°．
∴∠OBC=∠ABC-∠ABO=65°-25°=40°．
∵DO是AB的垂直平分线，AO为∠BAC的平分线，
∴点O是△ABC的外心，
∴OB=OC；
∴∠OCB=∠OBC=40°；
∵将∠C沿EF（E在BC上，F在AC上）折叠，点C与点O恰好重合，
∴OE=CE．
∴∠COE=∠OCB=40°；
在△OCE中，
∠OEC=180°-∠COE-∠OCB=180°-40°-40°=100°，
即∠OEC为 100度．
故选A

点评 该命题主要考查了翻折变换及其应用问题；解题的关键是根据翻折变换的性质找出图中隐含的等量关系，灵活运用有关定理来分析、判断、推理或解答．