练习册

  • 练习册
  • 试题
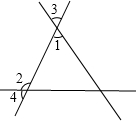
    精英家教网 > 初中数学 > 题目详情
    精英家教网如图，∠1=
    12
    ∠2，∠1+∠2=162°，求∠3与∠4的度数．
    分析：由已知∠1=
    1
    2
    ∠2，∠1+∠2=162°，可求∠1、∠2；又∠1与∠3是对顶角，∠4与∠2是邻补角，根据对顶角，邻补角的数量关系可求解．
    解答：解：由已知∠1=
    1
    2
    ∠2，∠1+∠2=162°，
    解得：∠1=54°，∠2=108°．
    ∵∠1与∠3是对顶角，
    ∴∠3=∠1=54°．
    ∵∠2与∠4是邻补角，
    ∴∠4=180°-∠2=72°．?
    点评：解决本题的关键是先求出∠1与∠2的度数，再利用对顶角，邻补角的性质求解．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

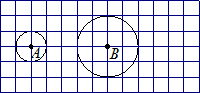    11、如图，在12×6的网格图中（每个小正方形的边长均为1个单位），⊙A的半径为1，⊙B的半径为2，要使⊙A与静止的⊙B相切，那么⊙A由图示位置需向右平移
    2、4、6或8
    个单位．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    精英家教网如图，用12米长的木方，做一个有一条横档的矩形窗子，为使透进的光线最多，选择窗子的长、宽各为
     
    、
     
    米．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    16、如图，在12×12的正方形网格中，△TAB的顶点坐标分别为T（1，1）、A（2，3）、B（4，2）
    （1）以点T（1，1）为位似中心，按比例尺（TA′：TA）=3：1在位似中心的同侧将△TAB放大为△TA′B′，放大后点A、B的对应点分别为A′、B′．画出△TA′B′，并写出点A′、B′的坐标；
    （2）在（1）中，若C（a，b）为线段AB上任一点，写出变化后点C的对应点C′的坐标．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    （2013•新余模拟）如图，共有12个大小相同的小正方形，其中阴影部分的5个小正方形是一个正方体的表面展开图的一部分，现从其余的小正方形中任取一个涂上阴影，能构成这个正方体的表面展开图的概率是
    4
    7
    4
    7
    ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

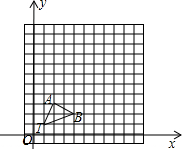    如图，在12×12的正方形网格中，△TAB的顶点坐标分别为T（1，1）、A（2，3）、B（4，2）．以点T（1，1）为位似中心，按比例尺TA′：TA=3：1在位似中心的同侧将△TAB放大为△TA′B′，放大后点A、B的对应点分别为A′、B′，画出△TA′B′，写出点A′、B′坐标．

    查看答案和解析>>

    同步练习册答案