
【题目】如图,在直角坐标系中,抛物线经过点A(0,4),B(1,0),C(5,0),其对称轴与x轴相交于点M.
(1)求抛物线的解析式和对称轴;
(2)在抛物线的对称轴上是否存在一点P,使△PAB的周长最小?若存在,请求出点P的坐标;若不存在,请说明理由;
(3)连接AC,在直线AC的下方的抛物线上,是否存在一点N,使△NAC的面积最大?若存在,请求出点N的坐标;若不存在,请说明理由.

【答案】(1)抛物线的解析式为y=![]() x2﹣
x2﹣![]() x+4,对称轴是:直线x=3;(2)P点坐标为(3,
x+4,对称轴是:直线x=3;(2)P点坐标为(3, ![]() ),
),
理由见解析;(3)在直线AC的下方的抛物线上存在点N(![]() ,﹣3),使△NAC面积最大.
,﹣3),使△NAC面积最大.
【解析】(1)根据已知条件可设抛物线的解析式为y=a(x-1)(x-5).
把点A(0,4)代入上式,解得a=![]() .
.
∴y=![]() (x-1)(x-5)=
(x-1)(x-5)=![]() x2-
x2-![]() x+4=
x+4=![]() (x-3)2-
(x-3)2-![]() .
.
∴抛物线的对称轴是x=3.
(2)存在,P点的坐标是(3, ![]() ).如图1,连接AC交对称轴于点P,连接BP,AB.
).如图1,连接AC交对称轴于点P,连接BP,AB.
∵点B与点C关于对称轴对称,
∴PB=PC.
∴AB+AP+PB=AB+AP+PC=AB+AC.
∴此时△PAB的周长最小.
设直线AC的解析式为y=kx+b.把A(0,4),C(5,0)代入y=kx+b,得
![]() 解得
解得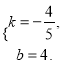
∴y=-![]() x+4.
x+4.
∵点P的横坐标为3,
∴y=-![]() ×3+4=
×3+4=![]() .
.
∴P(3, ![]() ).
).
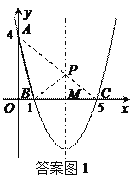

(3)在直线AC下方的抛物线上存在点N,使△NAC的面积最大.
如图2,设N点的横坐标为tt,此时点N(t, ![]() t2-
t2-![]() t+4)(0<t<5).
t+4)(0<t<5).
过点N作y轴的平行线,分别交x轴,AC于点F,G,过点A作AD⊥NG,垂足为D.
由(2)可知直线AC的解析式为y=-![]() x+4.
x+4.
把x=t代入y=-![]() x+4,得y=-
x+4,得y=-![]() t+4.
t+4.
∴G(t,- ![]() t+4).
t+4).
∴NG=-![]() t+4-(
t+4-(![]() t2-
t2-![]() t+4)=-
t+4)=-![]() t2+4t.
t2+4t.
∵AD+CF=OC=5,
∴S△NAC=S△ANG+S△CGN=![]() NG·AD+
NG·AD+![]() NG·CF=
NG·CF=![]() NG·OC
NG·OC
=![]() ×(-
×(-![]() t2+4t)×5=-2t2+10t=-2(t-
t2+4t)×5=-2t2+10t=-2(t-![]() )2+
)2+![]() .
.
∵当t=![]() 时,△NAC面积的最大值为
时,△NAC面积的最大值为![]() .
.
由t=![]() ,得y=
,得y=![]() ×(
×(![]() )2-
)2-![]() ×
×![]() +4=-3.
+4=-3.
∴N(![]() ,-3).
,-3).


 口算题天天练系列答案
口算题天天练系列答案科目:初中数学 来源: 题型:
【题目】三角形内有一点,它到三角形三边的距离都相等,同时与三角形三个顶点的距离也相等,则这个三角形一定是( )
A. 等腰三角形 B. 等腰直角三角形
C. 等边三角形 D. 以上都不对
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,过点A作AE⊥BC,垂足为E,连接DE,F为线段DE上一点,且∠AFE=∠B.
(1)求证:△ADF∽△DEC;
(2)若AB=8,AD=![]() ,AF=
,AF=![]() ,求AE的长.
,求AE的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数![]() 的图象与反比例函数
的图象与反比例函数![]() 的图象交于A(﹣2,m),B(4,﹣2)两点,与
的图象交于A(﹣2,m),B(4,﹣2)两点,与![]() 轴交于C点,过A作AD⊥
轴交于C点,过A作AD⊥![]() 轴于D.
轴于D.

(1)求这两个函数的解析式;
(2)求△ADC的面积.
(3)根据图象直接写出不等式![]() 的解集
的解集
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对下列说法谈谈你的看法:
(1)小明同学参加学校射击比赛,能否取得好成绩受很多因素的影响.所以在比赛前他的教练说他能获一等奖是没有道理的;
(2)天气预报说明天有雨,于是第二天一定下雨;
(3)班里分了一张参观根雕艺术展的门票,为了公平,班长让每个人来抽签决定.这样每个人抽得门票的概率都是50%.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com