
����Ŀ��A��һ�·ݲ�ֵΪ16��Ԫ����������ƣ��������·ݲ�ֵ����ƽ���½���Ϊx��0��x��1����B��һ�·ݲ�ֵΪ12��Ԫ�����·ݲ�ֵ�½���Ϊx�������������£����·ݲ�ֵ������������Ϊ2x�����·�A��B������ֵ�ֱ�ΪyA��yB����λ����Ԫ����
��1���ֱ�д��yA��yB��x�ĺ�������ʽ��
��2����yA=yBʱ����x��ֵ��
��3����xΪ��ֵʱ�����·�A��B������ֵ�IJ��������ֵ�Ƕ�����Ԫ��
���𰸡�
��1���⣺��������ɵã�yA=16��1��x��2��yB=12��1��x�� ��1+2x��
��2���⣺������� 16��1��x��2=12��1��x�� ��1+2x��
��ã�x1= ![]() ��x2=1��
��x2=1��
��0��x��1��
��x= ![]()
��3���⣺��0��x�� ![]() ʱ��yA��yB��
ʱ��yA��yB��
yA��yB=16��1��x��2��12��1��x�� ��1+2x��=40��x�� ![]() ��2��
��2�� ![]() ��
��
��x�� ![]() ʱ��yA��yB��ֵ��x���������С����0��x��
ʱ��yA��yB��ֵ��x���������С����0��x�� ![]() ��
��
�൱x=0ʱ��yA��yBȡ�����ֵ�����ֵΪ4��
�� ![]() ��x��1ʱ��yB��yA��
��x��1ʱ��yB��yA��
yB��yA=12��1��x�� ��1+2x����16��1��x��2=4��1��x����10x��1��=40��x�� ![]() ��2+
��2+ ![]() ��
��
�ߩ�40��0�� ![]() ��x��1��
��x��1��
�൱x= ![]() ʱ��yB��yAȡ���ֵ�����ֵΪ8.1��
ʱ��yB��yAȡ���ֵ�����ֵΪ8.1��
��8.1��4
�൱x= ![]() ʱ�����·�A��B������ֵ�IJ��������ֵ��8.1��Ԫ
ʱ�����·�A��B������ֵ�IJ��������ֵ��8.1��Ԫ
����������1�����������������ʵ���ȹ�ϵ��ʽ���ɣ���2���ɣ�1�������н���ʽ������yA=yB�з������ɵã���3����0��x�� ![]() ��
�� ![]() ��x��1���ö��κ��������ʽ��ɵã�
��x��1���ö��κ��������ʽ��ɵã�


 ��Ȥ����¹�֪��ϵ�д�
��Ȥ����¹�֪��ϵ�д� Ӣ��СӢ������Ĭдϵ�д�
Ӣ��СӢ������Ĭдϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������и��������������Ӧ�Ĵ������ڣ�
�٩�17���ڦУ��۩�|��![]() |����
|����![]() ����
����![]() ���ީ�0.92����
���ީ�0.92����![]() ���ੁ0.
���ੁ0.![]() ����1.2020020002��
����1.2020020002��
��1����ʵ��{�� ��}
��������{�� ��}
������{�� ��}
��2��������9������ѡȡ2����������2�����������á�+�����������¡��е�3�ֲ�ͬ��������Ž�ѡ����4�����������㣨���������ţ���ʹ�ü�����Ϊ���������г�ʽ�Ӳ������� ����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���Ķ���������֣�������⣺���֪��![]() ������������������������ѭ��С�������
������������������������ѭ��С�������![]() ��С���������Dz�����ȫ����д����������С����
��С���������Dz�����ȫ����д����������С����![]() ��1����ʾ
��1����ʾ![]() ��С�����֣���ʵ�ϣ�С���ı�ʾ�������е����ģ���Ϊ
��С�����֣���ʵ�ϣ�С���ı�ʾ�������е����ģ���Ϊ![]() ������������1�����������ȥ���������֣������
������������1�����������ȥ���������֣������![]() ��С�����֣������磺��22����
��С�����֣������磺��22����![]() ��2��32����2��
��2��32����2��![]() ��3����
��3����![]() ����������Ϊ2��С������Ϊ��
����������Ϊ2��С������Ϊ��![]() ��2����
��2����
����
��1��![]() �������������� �������������� ����
�������������� �������������� ����
��2�����![]() ��С������Ϊa��
��С������Ϊa��![]() ����������Ϊb����a+b��
����������Ϊb����a+b��![]() ��ֵ��
��ֵ��
��3����֪x��3+![]() ���������֣�y����С�����֣�ֱ��д��x��y��ֵ��
���������֣�y����С�����֣�ֱ��д��x��y��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij���г������̼ƻ�Ͷ��7.1��Ԫ����100��A�ͺ�30��B�����г�������B�ͳ�������A�ͳ����۵�6����60Ԫ��
��1����A��B�����ͺŵ����г����۷ֱ��Ƕ���Ԫ��
��2���������ڸþ������ʽ���ţ�Ͷ�빺�����ʽ���5.86��Ԫ��������������������������䣬��ô�����ܹ���B�ͳ���������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����壺�ڡ�ABC�У���C=30�㣬���ǰѡ�A�ĶԱ����C �ĶԱߵıȽ�����A�����ң�����thi A����thi A= ![]() =
= ![]() �������������⣺ ��֪���ڡ�ABC�У���C=30�㣮
�������������⣺ ��֪���ڡ�ABC�У���C=30�㣮
��1������A=45�㣬��thi A��ֵ��
��2����thi A= ![]() �����A=�㣻
�����A=�㣻
��3������A����ǣ�̽��thi A��sinA��������ϵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����һ��ֱ��������ֽƬBEC��б�߷��ھ���ABCD��BC���ϣ�ǡ����ȫ�غϣ�BE��CE�ֱ�AD�ڵ�F��G��BC=6��AF��FG��GD=3��2��1����AB�ij�Ϊ�� �� 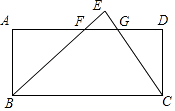
A.1
B.![]()
C.![]()
D.2
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
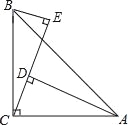
����Ŀ����ͼ����ACB=90����AC=BC��AD��CE��BE��CE������ֱ�ΪD��E��
��1��֤������BCE�ա�CAD��
��2����AD=25cm��BE=8cm����DE�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
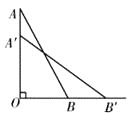
����Ŀ��һ��25�׳�������AB��б����һ��ֱ��ǽAO�ϣ���ʱ��AO����Ϊ24�ף�������ӵĶ���A��ǽ�»�4�ף���ô���ӵ�BҲ����4�ף�����Ϊʲô��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������y= ![]() x2+bx+c��y�ύ�ڵ�C��0����4������x�ύ�ڵ�A��B����B�������Ϊ��2��0����
x2+bx+c��y�ύ�ڵ�C��0����4������x�ύ�ڵ�A��B����B�������Ϊ��2��0����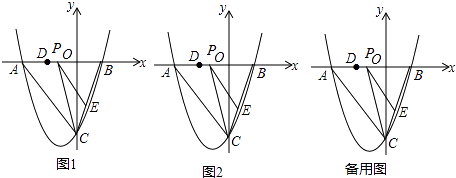
��1���������ߵĽ���ʽ��
��2������P��AB�ϵ�һ�����㣬����P��PE��AC��BC�ڵ�E������CP�����PCE������ʱP������ꣻ
��3���ڣ�2���������£�����DΪOA���е㣬��M���߶�AC��һ�㣬����OMDΪ����������ʱ������MP��ME���ѡ�MPE����PE���ۣ���M�Ķ�Ӧ��Ϊ��N��ֱ��д����N�����꣮
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com