
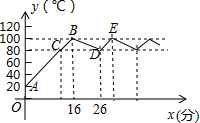
 ����ʦ�칫�ҵ���ˮ�������Զ����ڹ��ܣ��������Զ����м���״̬��ˮ��y���棩�뿪������ʱx�����ӣ���һ�κ�����ϵ����ˮ��������100��ʱֹͣ���ȣ�ˮ�¿�ʼ�½�����ʱˮ��y���棩�뿪������ʱx�����ӣ��Գ�һ�κ���ij���糿7��00ʱ������ʦ����ˮ����ˮ�±仯�����ͼ��ʾ��
����ʦ�칫�ҵ���ˮ�������Զ����ڹ��ܣ��������Զ����м���״̬��ˮ��y���棩�뿪������ʱx�����ӣ���һ�κ�����ϵ����ˮ��������100��ʱֹͣ���ȣ�ˮ�¿�ʼ�½�����ʱˮ��y���棩�뿪������ʱx�����ӣ��Գ�һ�κ���ij���糿7��00ʱ������ʦ����ˮ����ˮ�±仯�����ͼ��ʾ������ ��1�����߶�AB��������ʽΪy=kx+b����A��0��20����B��16��100������ⷽ���鼴�ɽ�����⣮
��2���ٵ�y=90�����x��ֵ���ɣ��ڸ���DE��AB�����ֱ��DE����ʽ���ɣ�
��3������˵������ʦ8��45ʱ�ص��칫�ҵ��¶Ⱥ�x=21ʱ���¶�һ��������߶�BD����ʽ���ɽ�����⣮
���  �⣺��1�����߶�AB��������ʽΪy=kx+b��
�⣺��1�����߶�AB��������ʽΪy=kx+b��
��A��0��20����B��16��100������$\left\{\begin{array}{l}{b=20}\\{16k+b=100}\end{array}\right.$
���$\left\{\begin{array}{l}{k=5}\\{b=20}\end{array}\right.$��
�����߶�AB�ĺ�������ʽy=5x+20��
��2����y=80ʱ��80=5x+20�����x=12��
���Կ�����12���ӣ�ˮ�µ�һ�δﵽ80�森
��������DE��AB�����߶�DE����ʽΪy=5x+b�䣬��D��26��80�������b��=-50��
�����߶�DE����ʽΪy=5x-50����y=100ʱ��100=5x-50�����x=30��
��������30���ӣ�ˮ�µڶ��δﵽ100�森
��3���߶�BD����ʽy=-2x+132��
�ߴ�B��D��E��ʱ����14���ӣ�
��105-30����14=5$\frac{5}{14}$��
������ʦ8��45ʱ�ص��칫�ҵ��¶Ⱥ�x=21ʱ���¶�һ����
x=21ʱ��y=-2��21+132=90��
������ʦ8��45ʱ�ص��칫��ʱ��ˮ���ڵ�ˮ��Ϊ90��C��
���� ���⿼��һ�κ�����Ӧ�á�����ϵ������֪ʶ������Ĺؼ���������ô���ϵ�����������������Ƴ�����ʦ8��45ʱ�ص��칫�ҵ��¶Ⱥ�x=21ʱ���¶�һ�����ǽ����ͻ�ƿڣ������п��������ͣ�


 ��ʦ�㲦��ϵ�д�
��ʦ�㲦��ϵ�д� Ӣ�żƻ���ĩ����ϵ�д�
Ӣ�żƻ���ĩ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
 ˫��̥�ֵ�С����С����ͬһ����飬����16��00ʱ��ѧ��С����ͬѧ��·�ؼң�;��û��ͣ����С���ﳵ�ؼң����Ǹ�����ѧУ�ľ���S���ף�����ȥ��ʱ��t�����ӣ��Ĺ�ϵ��ͼ��ʾ������ͼ���ṩ���й���Ϣ������˵���д�����ǣ�������
˫��̥�ֵ�С����С����ͬһ����飬����16��00ʱ��ѧ��С����ͬѧ��·�ؼң�;��û��ͣ����С���ﳵ�ؼң����Ǹ�����ѧУ�ľ���S���ף�����ȥ��ʱ��t�����ӣ��Ĺ�ϵ��ͼ��ʾ������ͼ���ṩ���й���Ϣ������˵���д�����ǣ�������| A�� | �ֵ����ļ���ѧУ1000�� | |
| B�� | ����ͬʱ���ң���ʱ30���� | |
| C�� | С�����ٶ�Ϊ50��/���� | |
| D�� | С���м�ͣ����һ��ʱ�������80��/���ӵ��ٶ���ؼ� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
 ��ƽ��ֱ������ϵ�У����ǰѺ������궼�������ĵ�������㣬��֪���κ���y=-$\frac{{x}^{2}}{3}$+4�ͷ���������y=$\frac{k}{x}$��k��0��x��0����ͼ����ͼ��ʾ������Χ�ɵ���Ӱ���֣������߽磩���������Ϊ5����k��ȡֵ��Χ�ǣ�������
��ƽ��ֱ������ϵ�У����ǰѺ������궼�������ĵ�������㣬��֪���κ���y=-$\frac{{x}^{2}}{3}$+4�ͷ���������y=$\frac{k}{x}$��k��0��x��0����ͼ����ͼ��ʾ������Χ�ɵ���Ӱ���֣������߽磩���������Ϊ5����k��ȡֵ��Χ�ǣ�������| A�� | 1��k��2 | B�� | 1��k��2 | C�� | 0��k��2 | D�� | 1��k��2 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��$\frac{a}{b}$=$\frac{c}{d}$����$\frac{a+c}{b+d}$=$\frac{c}{d}$ | B�� | ��$\frac{a}{b}$=$\frac{c}{d}$����$\frac{ax}{bx}$=$\frac{c}{d}$��x��0�� | ||
| C�� | ��$\frac{a}{b}$=$\frac{c}{d}$����$\frac{a��b}{b}$=$\frac{c��d}{d}$ | D�� | ��$\frac{a}{b}$=$\frac{c}{d}$����$\frac{a��1}{b}$=$\frac{c��1}{d}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��7��2�� | B�� | ��7��5�� | C�� | ��6��2�� | D�� | ��6��3�� |
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com