
分析 要求他一次性购买以上两次相同的商品,应付款多少元,就要先求出两次一共实际买了多少元,第一次购物有两种情况,也可能超过100,显然没有超过100,是按九折付款,也可能没有超过100,就是99元.第二次就有两种情况,一种是超过100元但不超过300元一律9折;一种是购物超过300元一律8折,依这两种计算出它购买的实际款数,再按第三种方案计算即是他应付款数.
解答 解:该人一次性购物付款99元,据条件(1)、(2)知他有可能享受九折优惠,则实际购物款为:99÷0.9=110元,也可能实际就是99元,没有优惠,故实际购物款为99元;
另一次购物付款252元,有两种可能,
其一购物超过300元按八折计,则实际购物款为$\frac{280}{0.8}$=350元.
其二购物超过100元但不超过300元按九折计算,则实际购物款为$\frac{280}{0.9}$=$\frac{2800}{9}$元.
故该人两次购物总价值为425元,390元,414元或379元,若一次性购买这些商品应付款为:
425×0.8=340元,
390×0.8=312元,
414×0.8=331.2元,
395×0.8=303.2元.
故答案为:303.2或312或331.2或340元.
点评 本题考查了打折销售的运用,分类讨论思想在数学实际问题中的运用,解答时分析清楚打折销售的几种情况是解答本题的关键.


科目:初中数学 来源: 题型:选择题
| A. | 平方等于本身的数只有0和1 | |
| B. | 两个负数,绝对值大的负数小 | |
| C. | 正数的绝对值是它本身,负数的绝对值是它的相反数 | |
| D. | 0除以任何数都得0 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | m+3<n+3 | B. | 9m<9n | C. | -m<-n | D. | $\frac{m}{2}$<$\frac{n}{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
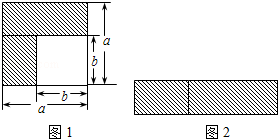
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,直线l1,l2交于点A,直线l2与x轴、y轴分别交于点B(-4,0)、D(0,4),直线l1所对应的函数关系式为y=-2x-2.
如图,直线l1,l2交于点A,直线l2与x轴、y轴分别交于点B(-4,0)、D(0,4),直线l1所对应的函数关系式为y=-2x-2.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
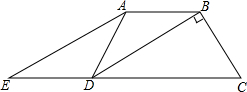 如图,在四边形ABCD中,AB=AD,BD平分∠ADC,E是CD的延长线上一点,且∠AEC=$\frac{1}{2}$∠ADC,求证:四边形ABDE是平行四边形.
如图,在四边形ABCD中,AB=AD,BD平分∠ADC,E是CD的延长线上一点,且∠AEC=$\frac{1}{2}$∠ADC,求证:四边形ABDE是平行四边形.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com