
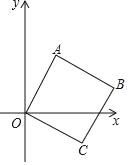
【题目】如图1,B(2m,0),C(3m,0)是平面直角坐标系中两点,其中m为常数,且m>0,E(0,n)为y轴上一动点,以BC为边在x轴上方作矩形ABCD,使AB=2BC,画射线OA,把△ADC绕点C逆时针旋转90°得△A′D′C′,连接ED′,抛物线![]() (
(![]() )过E,A′两点.
)过E,A′两点.

(1)填空:∠AOB= °,用m表示点A′的坐标:A′( , );
(2)当抛物线的顶点为A′,抛物线与线段AB交于点P,且![]() 时,△D′OE与△ABC是否相似?说明理由;
时,△D′OE与△ABC是否相似?说明理由;
(3)若E与原点O重合,抛物线与射线OA的另一个交点为点M,过M作MN⊥y轴,垂足为N:
①求a,b,m满足的关系式;
②当m为定值,抛物线与四边形ABCD有公共点,线段MN的最大值为10,请你探究a的取值范围.
【答案】(1)45;(m,﹣m);(2)相似;(3)①![]() ;②
;②![]() .
.
【解析】试题(1)由B与C的坐标求出OB与OC的长,进一步表示出BC的长,再证三角形AOB为等腰直角三角形,即可求出所求角的度数;由旋转的性质得,即可确定出A′坐标;
(2)△D′OE∽△ABC.表示出A与B的坐标,由![]() ,表示出P坐标,由抛物线的顶点为A′,表示出抛物线解析式,把点E坐标代入即可得到m与n的关系式,利用三角形相似即可得证;
,表示出P坐标,由抛物线的顶点为A′,表示出抛物线解析式,把点E坐标代入即可得到m与n的关系式,利用三角形相似即可得证;
(3)①当E与原点重合时,把A与E坐标代入![]() ,整理即可得到a,b,m的关系式;
,整理即可得到a,b,m的关系式;
②抛物线与四边形ABCD有公共点,可得出抛物线过点C时的开口最大,过点A时的开口最小,分两种情况考虑:若抛物线过点C(3m,0),此时MN的最大值为10,求出此时a的值;若抛物线过点A(2m,2m),求出此时a的值,即可确定出抛物线与四边形ABCD有公共点时a的范围.
试题解析:(1)∵B(2m,0),C(3m,0),∴OB=2m,OC=3m,即BC=m,∵AB=2BC,∴AB=2m=0B,∵∠ABO=90°,∴△ABO为等腰直角三角形,∴∠AOB=45°,由旋转的性质得:OD′=D′A′=m,即A′(m,﹣m);故答案为:45;m,﹣m;
(2)△D′OE∽△ABC,理由如下:由已知得:A(2m,2m),B(2m,0),∵![]() ,∴P(2m,
,∴P(2m, ![]() m),∵A′为抛物线的顶点,∴设抛物线解析式为
m),∵A′为抛物线的顶点,∴设抛物线解析式为![]() ,∵抛物线过点E(0,n),∴
,∵抛物线过点E(0,n),∴![]() ,即m=2n,∴OE:OD′=BC:AB=1:2,∵∠EOD′=∠ABC=90°,∴△D′OE∽△ABC;
,即m=2n,∴OE:OD′=BC:AB=1:2,∵∠EOD′=∠ABC=90°,∴△D′OE∽△ABC;
(3)①当点E与点O重合时,E(0,0),∵抛物线![]() 过点E,A,∴
过点E,A,∴![]() ,整理得:
,整理得: ![]() ,即
,即![]() ;
;
②∵抛物线与四边形ABCD有公共点,∴抛物线过点C时的开口最大,过点A时的开口最小,若抛物线过点C(3m,0),此时MN的最大值为10,∴a(3m)2﹣(1+am)3m=0,整理得:am=![]() span>,即抛物线解析式为
span>,即抛物线解析式为![]() ,由A(2m,2m),可得直线OA解析式为y=x,联立抛物线与直线OA解析式得:
,由A(2m,2m),可得直线OA解析式为y=x,联立抛物线与直线OA解析式得:  ,解得:x=5m,y=5m,即M(5m,5m),令5m=10,即m=2,当m=2时,a=
,解得:x=5m,y=5m,即M(5m,5m),令5m=10,即m=2,当m=2时,a=![]() ;
;
若抛物线过点A(2m,2m),则![]() ,解得:am=2,∵m=2,∴a=1,则抛物线与四边形ABCD有公共点时a的范围为
,解得:am=2,∵m=2,∴a=1,则抛物线与四边形ABCD有公共点时a的范围为![]() .
.


科目:初中数学 来源: 题型:
【题目】为了节约水资源,某市准备按照居民家庭年用水量实行阶梯水价,水价分档递增,计划使第一档、第二档和第三档的水价分别覆盖全市居民家庭的80%,15%和5%.为合理确定各档之间的界限,随机抽查了该市5万户居民家庭上一年的年用水量(单位:m3),绘制了统计图,如图所示.下面有四个推断:

①年用水量不超过180m3的该市居民家庭按第一档水价交费;
②年用水量不超过240m3的该市居民家庭按第三档水价交费;
③该市居民家庭年用水量的中位数在150~180m3之间;
④该市居民家庭年用水量的众数约为110m3.
其中合理的是( )
A. ①③ B. ①④ C. ②③ D. ②④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,菱形、矩形与正方形的形状有差异,我们将菱形、矩形与正方形的接近程度称为“接近度”.在研究“接近度”时,应保证相似图形的“接近度”相等.
(1)设菱形相邻两个内角的度数分别为![]() 和
和![]() ,将菱形的“接近度”定义为
,将菱形的“接近度”定义为![]() ,于是,
,于是,![]() 越小,菱形越接近于正方形.
越小,菱形越接近于正方形.
①若菱形的一个内角为![]() ,则该菱形的“接近度”等于 ;
,则该菱形的“接近度”等于 ;
②当菱形的“接近度”等于 时,菱形是正方形.

(2)设矩形相邻两条边长分别是![]() 和
和![]() (
(![]() ),将矩形的“接近度”定义为
),将矩形的“接近度”定义为![]() ,于是
,于是![]() 越小,矩形越接近于正方形.
越小,矩形越接近于正方形.
你认为这种说法是否合理?若不合理,给出矩形的“接近度”一个合理定义.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将边长为2cm的正方形OABC放在平面直角坐标系中,O是原点,点A的横坐标为1,则点C的坐标为( )
A. (![]() ,-1) B. (2,﹣1) C. (1,-
,-1) B. (2,﹣1) C. (1,-![]() ) D. (﹣1,
) D. (﹣1,![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】京张高铁是世界上首条智能化高速铁路,起点是北京北,终点是张家口南.建成后的京张高铁铁路运行里程由原来的196km缩短为174km,运行时间缩短为原来的![]() ,平均速度比原来快150千米/小时.求建成后的京张高铁从北京北至张家口南的运行时间.
,平均速度比原来快150千米/小时.求建成后的京张高铁从北京北至张家口南的运行时间.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知如图,点A、点B在直线l异侧,以点A为圆心,AB长为半径作弧交直线l于C、D两点.分别以C、D为圆心,AB长为半径作弧,两弧在l下方交于点E,连结AE.
(1)根据题意,利用直尺和圆规补全图形;
(2)证明:l垂直平分AE.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列各变量之间是反比例关系的是( )
A. 存入银行的利息和本金 B. 在耕地面积一定的情况下,人均占有耕地面积与人口数
C. 汽车行驶的时间与速度 D. 电线的长度与其质量
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“元旦”期间小明去永辉超市购物,恰逢永辉超市“满1400减99元”促销活动,小明准备提前购置一些年货![]() 和
和![]() ,已知
,已知![]() 和
和![]() 的单价总和是100到200之间的整数,小明粗略测算了一下发现自己所购年货总价为1305元,不能达到超市的促销活动金额. 于是小明又购买了
的单价总和是100到200之间的整数,小明粗略测算了一下发现自己所购年货总价为1305元,不能达到超市的促销活动金额. 于是小明又购买了![]() 、
、![]() 各一件,这样就能参加超市的促销活动,最后刚好付款1305元. 小明经仔细计算发现前面粗略测算时把
各一件,这样就能参加超市的促销活动,最后刚好付款1305元. 小明经仔细计算发现前面粗略测算时把![]() 和
和![]() 的单价看反了,那么小明实际总共买了______件年货.
的单价看反了,那么小明实际总共买了______件年货.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com