解:(1)因为y=-x
2+2kx-k
2+k+1=-(x-k)
2+k+1,
所以抛物线的顶点坐标是(k,k+1),对称轴是x=k.
(2)因为抛物线的顶点为(k,k+1),
所以

,
消去k得,y=x+1
由此可见,不论k取任何实数,抛物线的顶点(k,k+1)都满足函数y=x+1,
即在一次函数y=x+1的图象上.
所以函数y=x+1是所求函数的解析式.
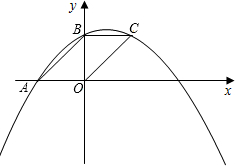
(3)符合条件的点P存在.
因为点A(0,1)_在抛物线上,
所以,1=-k
2+k+1,
解得k=0或k=1,
①当k=0时,k+1=1,所以它的顶点是B(0,1)与点A重合,不合题意,舍去.所以k≠0
②当k=1时,k+1=2,他的顶点为B(1,2),
因为点A、B已经确定,所以AB的长度为定值,
所以要使△ABP的周长最小,只须AP+PB的和最小.
此时,取AP+PB最小,所以点P为所求的点,
设直线A′B的解析式为y=ax+b,它过点A′(0,-1),B(1,2),
所以

,
解得
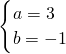
,
所以y=3x-1,
因为点P在x轴上,所以当y=0时,x=

,
所以当点p的坐标为(

,0)时,△ABP的周长最小.
分析:(1)把函数关系式化为顶点式y=-x
2+2kx=k
2+k+1=-(x-k)
2+k+1,可得抛物线的顶点坐标是(k,k+1),对称轴是x=k.
(2)因把抛物线的顶点(k,k+1),写成方程组

,消去k得,y=x+1,由此可见函数y=x+1是所求函数的解析式.
(3)把点A(0,1),代入二次函数可知,1=-k
2+k+1,解得k=0或k=1,分别把k值代入题中确定,当k=1时,k+1=2,他的顶点为B(1,2),取AP+PB最小,点P为所求的点.设直线A′B的解析式为y=ax+b,把点A′(0,-1),B(1,2),代入解析式可得

,解得y=3x-1,因为点P在x轴上,所以当y=0时,x=

,所以当点p的坐标为(

,0)时,△ABP的周长最小.
点评:本题是二次函数的综合题型,其中涉及的知识点有抛物线的顶点公式和待定系数法求函数解析式的方法以及线段和的最小值问题.注意分析题意分情况讨论结果.

 ABP的周长最小?若存在,请求出点P的坐标;若不存在,请简述理由.
ABP的周长最小?若存在,请求出点P的坐标;若不存在,请简述理由. ,
, ,
,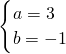 ,
, ,
, ,0)时,△ABP的周长最小.
,0)时,△ABP的周长最小. ,消去k得,y=x+1,由此可见函数y=x+1是所求函数的解析式.
,消去k得,y=x+1,由此可见函数y=x+1是所求函数的解析式. ,解得y=3x-1,因为点P在x轴上,所以当y=0时,x=
,解得y=3x-1,因为点P在x轴上,所以当y=0时,x= ,所以当点p的坐标为(
,所以当点p的坐标为( ,0)时,△ABP的周长最小.
,0)时,△ABP的周长最小.

 (1)求b+c的值;
(1)求b+c的值;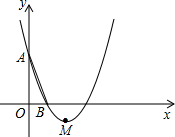 (2012•虹口区一模)如图,在平面直角坐标系xOy中,已知抛物线y=x2+bx+c经过A(0,3),B(1,0)两点,顶点为M.
(2012•虹口区一模)如图,在平面直角坐标系xOy中,已知抛物线y=x2+bx+c经过A(0,3),B(1,0)两点,顶点为M.