
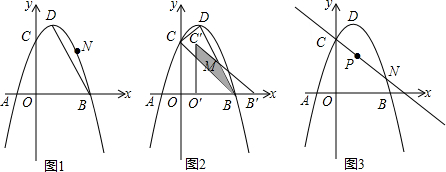
分析 (1)用待定系数法求直线和抛物线解析式;
(2)根据BC∥B′C′和平移,得到直线B′C′解析式为y=-(x-m)+3=-x+3+m,再联立$\left\{\begin{array}{l}{y=-2x+6}\\{y=-x+3+m}\end{array}\right.$,求得交点坐标,从而确定出T,而T=$\frac{1}{3}$S△OBC,求得BM;
(3)先求出直线CN的解析式为y=-$\frac{1}{2}$x+3,分三种情况,再由点Q既在抛物线y=-x2+2x+3上,又在直线CN为y=-$\frac{1}{2}$x+3上,确定出m即可.
解答 解:(1)将点A(-1,0)代入抛物线y=-x2+2x+c中得:
0=-1-2+c,解得:c=3,
∴抛物线y=-x2+2x+3=-(x-3)(x+1)=-(x-1)2+4,
∴点B坐标为(3,0),点D坐标为(1,4).
设直线BD的解析式为y=kx+b,
则有$\left\{\begin{array}{l}{0=3k+b}\\{4=k+b}\end{array}\right.$,解得:$\left\{\begin{array}{l}{k=-2}\\{b=6}\end{array}\right.$.
∴直线BD的解析式为y=-2x+6.
(2)∵B(3,0),C(0,3),
直线BC解析式为y=-x+3,
∵BC∥B′C′,
kB′C′=-1,
设平移距离为m,
∴0<m<$\frac{3}{2}$,
∴直线B′C′解析式为y=-(x-m)+3=-x+3+m,
∴O′(m,0)
∴O′C′与BC的交点E(m,3-m),
∴EO′=BO′=3-m,
∴$\left\{\begin{array}{l}{y=-2x+6}\\{y=-x+3+m}\end{array}\right.$,
∴$\left\{\begin{array}{l}{x=3-m}\\{y=2m}\end{array}\right.$,
∴T=S△B′O′C′-S△BB′N-S△BO′E
=$\frac{9}{2}$-m×2m×$\frac{1}{2}$-$\frac{1}{2}$(3-m)2
=-$\frac{3}{2}$m2+3m,
∵T=$\frac{1}{3}$S△OBC,
∴-$\frac{3}{2}$m2+3=$\frac{1}{3}$×$\frac{9}{2}$,
∴m=1,
∴M(2,2),
∴BM=$\sqrt{5}$,
(3)如图,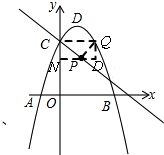
当x=$\frac{5}{2}$时,y=$\frac{7}{4}$,
∴N($\frac{5}{2}$,$\frac{7}{4}$),
∵C(0,3),
∴直线CN解析式为y=-$\frac{1}{2}$x+3
①∠PCQ=90°,
∴CQ⊥CN,
∴直线CQ解析式为y=2x+3,
∵$\left\{\begin{array}{l}{y=2x+3}\\{y=-{x}^{2}+2x+3}\end{array}\right.$,
∴$\left\{\begin{array}{l}{x=0}\\{y=3}\end{array}\right.$,
∴CQ与抛物线仅一个交点,不满足题意;
②当∠CPQ=90°时,
∵CP=PQ,∠CFP=∠PEQ=90°,∠CPF=∠PQE,
∴△CFP≌△PEQ,
∴CF=PE,PF=QE,
设P(m,-$\frac{1}{2}$m+3),
∴PE=CF=$\frac{1}{2}$m,QE=PF=m,
Ⅰ、∴Q点的横坐标为PE+PF=$\frac{3}{2}$m,纵坐标为-$\frac{1}{2}$m+3+m=$\frac{1}{2}$m+3
∴Q($\frac{3m}{2}$,3),
∴$\frac{1}{2}$m+3=-($\frac{3m}{2}$)2+2×$\frac{3m}{2}$+3,
∴m=0(舍)或m=$\frac{10}{9}$,
∴P($\frac{10}{9}$,$\frac{22}{9}$)
∵C(0,3),
∴CP=$\frac{5\sqrt{5}}{9}$
Ⅱ、点Q在第四象限内,同Ⅰ的方法得出Q($\frac{1}{2}$m,-$\frac{3}{2}$m+3),
∴-$\frac{3}{2}$m+3=-($\frac{1}{2}$m)2+2×$\frac{1}{2}$m+3,
∴m=0(舍)或m=10,
∴P(10,-2),
∴CP=5$\sqrt{5}$,
③当∠CQP=90°,CQ=QP时,方法同上,
CP=$\frac{10\sqrt{5}}{9}$或CP=10$\sqrt{5}$;
即:CP的长度为$\frac{5\sqrt{5}}{9}$、$5\sqrt{5}$、$\frac{{10\sqrt{5}}}{9}$、$10\sqrt{5}$.
点评 此题是二次函数综合题,主要考查了待定系数法求函数解析式,求直线和抛物线的交点坐标,解本题的关键是求直线和抛物线的交点坐标,也是本题的难点.


 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案科目:初中数学 来源: 题型:填空题
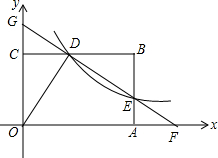 如图,反比例函数y=$\frac{4}{x}$(x>0)的图象与矩形ABCO的边BC交于点D,与边AB交与点E,直线DE与x轴、y轴分别交于点F、G.若△ODG与△ODF的面积比为2:7,则矩形ABCO的面积是14.
如图,反比例函数y=$\frac{4}{x}$(x>0)的图象与矩形ABCO的边BC交于点D,与边AB交与点E,直线DE与x轴、y轴分别交于点F、G.若△ODG与△ODF的面积比为2:7,则矩形ABCO的面积是14.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
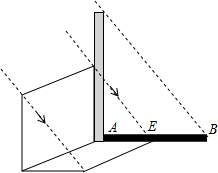 如图,一块长方形木板紧靠着一根直立于地面的木杆,其中木杆在太阳光下的投影已经画出(图中线段AB),画出此时长方形木板在地面上的投影示意图.
如图,一块长方形木板紧靠着一根直立于地面的木杆,其中木杆在太阳光下的投影已经画出(图中线段AB),画出此时长方形木板在地面上的投影示意图.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com