
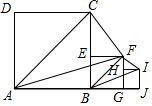
 如图,已知四边形ABCD,BEFG,GHIJ都是正方形,E为BC边上的动点,H为FG的中点,若AB=1,记BE=x,△ACF与△BFI的面积之和为y,则y关于x的函数图象正确的是( )
如图,已知四边形ABCD,BEFG,GHIJ都是正方形,E为BC边上的动点,H为FG的中点,若AB=1,记BE=x,△ACF与△BFI的面积之和为y,则y关于x的函数图象正确的是( )| A. | 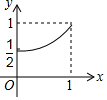 | B. | 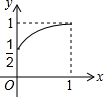 | C. | 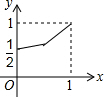 | D. | 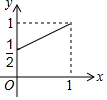 |
分析 根据正方形的性质得到AB=BC,BE=BG=GF,GJ=JI=GH,根据图形的面积公式得到y=S△ABC+S△CFE+S正方形BGFE-S△AGF+S△BJI,于是得到结论.
解答  解:∵AB=1,BE=x,
解:∵AB=1,BE=x,
∴CE=1-x,
∵H为FG的中点,
∴GH=$\frac{1}{2}$x,
∵四边形ABCD,BEFG,GHIJ都是正方形,
∴AB=BC,BE=BG=GF,GJ=JI=GH,
∴y=S△ABC+S△CFE+S正方形BGFE-S△AGF+S△BJI=$\frac{1}{2}×$1×1+$\frac{1}{2}$•x•(1-x)+x2-$\frac{1}{2}$×(1+x)•x+$\frac{1}{2}$•$\frac{3}{2}$x•$\frac{1}{2}$x,
即y=$\frac{3}{8}$x2-x+$\frac{1}{2}$,
∴y关于x的函数图象正确的是A,
故选A.
点评 本题考查了动点问题的函数图象,图形的面积的计算,正方形的性质,正确的识别图形是解题的关键.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{1}{2^{98}}$尺 | B. | $\frac{1}{2^{99}}$尺 | C. | $\frac{1}{2^{100}}$尺 | D. | $\frac{1}{{2}^{101}}$尺 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com