
【题目】已知:如图,在□ABCD中,AE是BC边上的高,将![]() 沿
沿![]() 方向平移,使点E与点C重合,得
方向平移,使点E与点C重合,得![]() .
.

(1)求证:![]() ;
;
(2)若![]() ,当AB与BC满足什么数量关系时,四边形
,当AB与BC满足什么数量关系时,四边形![]() 是菱形?并说明理由.
是菱形?并说明理由.
注:(直角三角形中30°角所对直角边等于斜边的一半).
【答案】(1)证明见解析;(2)当BC=![]() AB时,四边形ABFG是菱形.
AB时,四边形ABFG是菱形.
【解析】
试题分析:(1)根据平移的性质,可得:BE=FC,再证明Rt△ABE≌Rt△CDG可得:DG=FC;即可得到BE=DG;
(2)要使四边形ABFG是菱形,须使AB=BF;根据条件找到满足AB=BF的AB与BC满足的数量关系即可.
试题解析:(1)∵四边形ABCD是平行四边形,
∴AB=CD.
∵AE是BC边上的高,且CG是由AE沿BC方向平移而成.
∴CG⊥AD.
∴∠AEB=∠CGD=90°.
∵AE=CG,AB=CD,
∴Rt△ABE≌Rt△CDG.
∴BE=DG;
(2)当BC=![]() AB时,四边形ABFG是菱形.
AB时,四边形ABFG是菱形.
证明:∵AB∥GF,AG∥BF,
∴四边形ABFG是平行四边形.
∵Rt△ABE中,∠B=60°,
∴∠BAE=30°,
∴BE=![]() AB.(直角三角形中30°所对直角边等于斜边的一半)
AB.(直角三角形中30°所对直角边等于斜边的一半)
∵BE=CF,BC=![]() AB,
AB,
∴EF=![]() AB.
AB.
∴AB=BF.
∴四边形ABFG是菱形.


 状元坊全程突破导练测系列答案
状元坊全程突破导练测系列答案科目:初中数学 来源: 题型:
【题目】(1)如图①,一个无盖的长方体盒子的棱长分别为![]() ,
,![]() ,
,![]() ,盒子的内部顶点
,盒子的内部顶点![]() 处有一只昆虫甲,在盒子的内部顶点
处有一只昆虫甲,在盒子的内部顶点![]() 处有一只昆虫乙(盒壁的厚度忽略不计)假设昆虫甲在顶点
处有一只昆虫乙(盒壁的厚度忽略不计)假设昆虫甲在顶点![]() 处静止不动,请计算
处静止不动,请计算![]() 处的昆虫乙沿盒子内壁爬行到昆虫甲
处的昆虫乙沿盒子内壁爬行到昆虫甲![]() 处的最短路程,并画出其最短路径,简要说明画法
处的最短路程,并画出其最短路径,简要说明画法
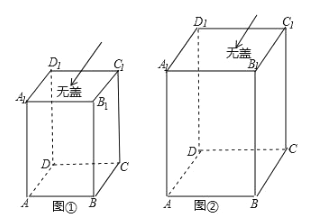
(2)如果(1)问中的长方体的棱长分别为![]() ,
,![]() ,如图②,假设昆虫甲从盒内顶点
,如图②,假设昆虫甲从盒内顶点![]() 以1厘米/秒的速度在盒子的内部沿棱
以1厘米/秒的速度在盒子的内部沿棱![]() 向下爬行,同时昆虫乙从盒内顶点
向下爬行,同时昆虫乙从盒内顶点![]() 以3厘米/秒的速度在盒壁的侧面上爬行,那么昆虫乙至少需要多长时间才能捕捉到昆虫甲?
以3厘米/秒的速度在盒壁的侧面上爬行,那么昆虫乙至少需要多长时间才能捕捉到昆虫甲?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市从2018年开始大力发展旅游产业.据统计,该市2018年旅游收入约为2亿元.预计2020年旅游收入约达到2.88亿元,设该市旅游收入的年平均增长率为x,下面所列方程正确的是( )
A. 2(1+x)2=2.88 B. 2x2=2.88 C. 2(1+x%)2=2.88 D. 2(1+x)+2(1+x)2=2.88
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】太阳与地球的平均距离大约是150 000 000千米,数据150 000 000用科学记数法表示为( )
A.1.5×108
B.1.5×109
C.0.15×109
D.15×107
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,点E是AD的中点,∠EBC的平分线交CD于点F.将△DEF沿EF折叠,点D恰好落在BE上M点处,延长BC、EF交于点N, 有下列四个结论:① DF=CF;② BF⊥EN;③△BEN是等边三角形;④ S△BEF=3S△DEF. 其中,正确的结论有( )
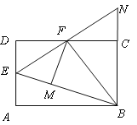
A.1个 B.2个 C.3个 D.4个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com