
 ��ͼ����֪������y=$\frac{1}{3}$x2+bx+c������ABC���������㣬���е�A��0��1������B��-9��10����AC��x�ᣬ��P��ֱ��AC�·��������ϵĶ��㣮
��ͼ����֪������y=$\frac{1}{3}$x2+bx+c������ABC���������㣬���е�A��0��1������B��-9��10����AC��x�ᣬ��P��ֱ��AC�·��������ϵĶ��㣮���� ��1���ô���ϵ������������߽���ʽ���ɣ�
��2�����P��m��$\frac{1}{3}$m2+2m+1������ʾ��PE=-$\frac{1}{3}$m2-3m������S�ı���AECP=S��AEC+S��APC=$\frac{1}{2}$AC��PE������������ϵʽ�������ֵ���ɣ�
��3�����жϳ�PF=CF���ٵõ���PCA=��EAC����C��P��QΪ��������������ABC���ƣ�������������㼴�ɣ�
��� �⣺��1���ߵ�A��0��1����B��-9��10�����������ϣ�
��$\left\{\begin{array}{l}{c=1}\\{\frac{1}{3}��81-9b+c=10}\end{array}\right.$��
��$\left\{\begin{array}{l}{b=2}\\{c=1}\end{array}\right.$��
�������ߵĽ���ʽΪy=$\frac{1}{3}$x2+2x+1��
��2����AC��x�ᣬA��0��1��
��$\frac{1}{3}$x2+2x+1=1��
��x1=-6��x2=0��
���C�����꣨-6��1����
�ߵ�A��0��1����B��-9��10����
��ֱ��AB�Ľ���ʽΪy=-x+1��
���P��m��$\frac{1}{3}$m2+2m+1��
��E��m��-m+1��
��PE=-m+1-��$\frac{1}{3}$m2+2m+1��=-$\frac{1}{3}$m2-3m��
��AC��EP��AC=6��
��S�ı���AECP
=S��AEC+S��APC
=$\frac{1}{2}$AC��EF+$\frac{1}{2}$AC��PF
=$\frac{1}{2}$AC����EF+PF��
=$\frac{1}{2}$AC��PE
=$\frac{1}{2}$��6����-$\frac{1}{3}$m2-3m��
=-m2-9m
=-��m+$\frac{9}{2}$��2+$\frac{81}{4}$��
��-6��m��0
�൱m=-$\frac{9}{2}$ʱ���ı���AECP����������ֵ��$\frac{81}{4}$��
��ʱ��P��-$\frac{9}{2}$��-$\frac{5}{4}$����
��3����y=$\frac{1}{3}$x2+2x+1=$\frac{1}{3}$��x+3��2-2��
��P��-3��-2����
��PF=yF-yP=3��CF=xF-xC=3��
��PF=CF��
���PCF=45��
ͬ���ɵã���EAF=45�㣬
���PCF=��EAF��
����ֱ��AC�ϴ�������������Q��
��Q��t��1����AB=9$\sqrt{2}$��AC=6��CP=3$\sqrt{2}$
����C��P��QΪ��������������ABC���ƣ�
�ٵ���CPQ�ס�ABCʱ��
��$\frac{CQ}{AC}=\frac{CP}{AB}$��
��$\frac{|t+6|}{6}=\frac{3\sqrt{2}}{9\sqrt{2}}$��
��t=-4��t=-8�����������⣬�ᣩ
��Q��-4��1��
�ڵ���CQP�ס�ABCʱ��
��$\frac{CQ}{AB}=\frac{CP}{AC}$��
��$\frac{|t+6|}{9\sqrt{2}}=\frac{3\sqrt{2}}{6}$��
��t=3��t=-15�����������⣬�ᣩ
��Q��3��1��
���� �����Ƕ��κ����ۺ��⣬��Ҫ�����˴���ϵ���������������ε����ʣ�����ͼ����������ø�������Ȿ��Ĺؼ�����������ʽ��


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | x��1 | B�� | x��1 | C�� | x��1��x��3 | D�� | x��3 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | x��$-\frac{3}{2}$ | B�� | x��-$\frac{3}{2}$ | C�� | x��-$\frac{2}{3}$ | D�� | x��-$\frac{2}{3}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
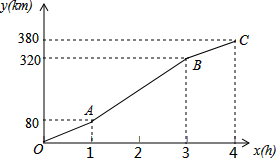 ����ڼ䣬С��һ�ҳ˳�ȥ���380�����ij�������Σ�������ҵľ���y��km����������ʻʱ��x��h��֮��ĺ���ͼ����ͼ��ʾ��
����ڼ䣬С��һ�ҳ˳�ȥ���380�����ij�������Σ�������ҵľ���y��km����������ʻʱ��x��h��֮��ĺ���ͼ����ͼ��ʾ���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
 ��ͼ����ƽ��ֱ������ϵ�У���M��x�������ڵ�A��8��0������y��ֱ��ڵ�B��0��4���͵�C��0��16������Բ��M������ԭ��O�ľ����ǣ�������
��ͼ����ƽ��ֱ������ϵ�У���M��x�������ڵ�A��8��0������y��ֱ��ڵ�B��0��4���͵�C��0��16������Բ��M������ԭ��O�ľ����ǣ�������| A�� | 10 | B�� | 8$\sqrt{2}$ | C�� | 4$\sqrt{13}$ | D�� | 2$\sqrt{41}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
 ��ͼ��������ֽƬABCD�У��Խ���AC��BD���ڵ�O���۵�������ֽƬABCD��ʹAD����BD�ϣ���Aǡ����BD�ϵĵ�F�غϣ�չ�����ۺ�DE�ֱ�AB��AC�ڵ�E��G������GF���������н��ۣ��١�ADG=22.5�㣻��tan��AED=2����S��AGD=S��OGD�����ı���AEFG�����Σ���BE=2OG������S��OGF=1����������ABCD�������6+4$\sqrt{2}$��������ȷ�Ľ��۸���Ϊ��������
��ͼ��������ֽƬABCD�У��Խ���AC��BD���ڵ�O���۵�������ֽƬABCD��ʹAD����BD�ϣ���Aǡ����BD�ϵĵ�F�غϣ�չ�����ۺ�DE�ֱ�AB��AC�ڵ�E��G������GF���������н��ۣ��١�ADG=22.5�㣻��tan��AED=2����S��AGD=S��OGD�����ı���AEFG�����Σ���BE=2OG������S��OGF=1����������ABCD�������6+4$\sqrt{2}$��������ȷ�Ľ��۸���Ϊ��������| A�� | 2 | B�� | 3 | C�� | 4 | D�� | 5 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 1-$\frac{1}{x}$ | B�� | $\frac{{x}^{2}-1}{x}$•$\frac{x}{x+1}$ | C�� | $\frac{x+1}{x}$��$\frac{1}{x-1}$ | D�� | $\frac{{x}^{2}+2x+1}{x+1}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com