
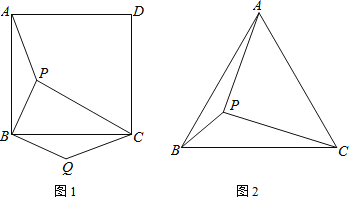
【题目】(1)如图1,点P是正方形ABCD内的一点,把△ABP绕点B顺时针方向旋转,使点A与点C重合,点P的对应点是Q.若PA=3,PB=2![]() ,PC=5,求∠BQC的度数.
,PC=5,求∠BQC的度数.
(2)点P是等边三角形ABC内的一点,若PA=12,PB=5,PC=13,求∠BPA的度数.
【答案】(1)135°;(2)150°
【解析】
(1)根据题意得出△ABP绕点B顺时针方向旋转了90°,才使点A与C重合,进而得出∠PBQ=90°,再利用勾股定理得出∠PQC的度数,进而求出∠BQC的度数;
(2)将△ABP绕点B顺时针方向旋转60°得到△CBP',由旋转知,△APB≌△CP'B,即∠BPA=∠BP'C,P'B=PB=5,P'C=PA=12,进而得出△PBP'也是正三角形,即∠PP'B=60°,PP'=5.
在△PP'C中,由勾股定理的逆定理得出∠PP'C=90°,从而可以得出结论.
(1)连接PQ.
由旋转可知:![]() ,QC=PA=3.
,QC=PA=3.
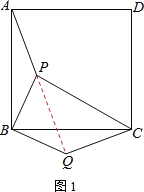
又∵ABCD是正方形,
∴△ABP绕点B顺时针方向旋转了90°,才使点A与C重合,
即∠PBQ=90°,∴∠PQB=45°,PQ=4.
则在△PQC中,PQ=4,QC=3,PC=5,∴PC2=PQ2+QC2.
即∠PQC=90°.
故∠BQC=90°+45°=135°.
(2)将△ABP绕点B顺时针方向旋转60°得到△CBP',
此时点P的对应点是点P'.
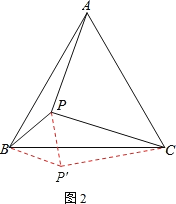
由旋转知,△APB≌△CP'B,即∠BPA=∠BP'C,P'B=PB=5,P'C=PA=12.
又∵△ABC是正三角形,∴∠ABP+∠PBC=60°,
∴∠CBP'+∠PBC=60°,∴∠PBP'=60°.
又∵P'B=PB=5,∴△PBP'也是正三角形,即∠PP'B=60°,PP'=5.
在△PP'C中,∵PC=13,PP'=5,P'C=12,∴PC2=PP'2+P'C2.
即∠PP'C=90°.
故∠BPA=∠BP'C=60°+90°=150°.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案 目标测试系列答案
目标测试系列答案科目:初中数学 来源: 题型:
【题目】已知y=ax2+bx+c(其中a,b,c为常数,且a≠0),乐老师在用描点法画其的图象时,列出如下表格,根据该表格,下列判断中不正确的是( )
x | … | ﹣1 | 0 | 1 | 2 | … |
y | … | ﹣2 | 2.5 | 4 | 2.5 | … |
A. a<0
B. 一元二次方程ax2+bx+c﹣5=0没有实数根
C. 当x=3时y=﹣2
D. 一元二次方程ax2+bx+c=0有一根比3大
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两所医院分别有一男一女共4名医护人员支援湖北武汉抗击疫情.
(1)若从甲、乙两医院支援的医护人员中分别随机选1名,则所选的2名医护人员性别相同的概率是 ;
(2)若从支援的4名医护人员中随机选2名,用列表或画树状图的方法求出这2名医护人员来自同一所医院的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知AB是⊙O的直径,C为⊙O上一点,∠OAC=58°.

(Ⅰ)如图①,过点C作⊙O的切线,与BA的延长线交于点P,求∠P的大小;
(Ⅱ)如图②,P为AB上一点,CP延长线与⊙O交于点Q.若AQ=CQ,求∠APC的大小.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知⊙O的半径为2,AB为直径,CD为弦,AB与CD交于点M,将弧CD沿着CD翻折后,点A与圆心O重合,延长OA至P,使AP=OA,链接PC。

(1)求CD的长;
(2)求证:PC是⊙O的切线;
(3)点G为弧ADB的中点,在PC延长线上有一动点Q,连接QG交AB于点E,交弧BC于点F(F与B、C不重合)。问GEGF是否为定值?如果是,求出该定值;如果不是,请说明理由。
查看答案和解析>>
科目:初中数学 来源: 题型:
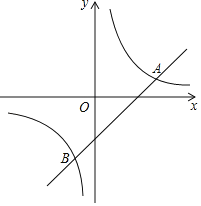
【题目】如图,在平面直角坐标系xOy中,直线y=x﹣2与双曲线y=![]() (k≠0)相交于A,B两点,且点A的横坐标是3.
(k≠0)相交于A,B两点,且点A的横坐标是3.
(1)求k的值;
(2)过点P(0,n)作直线,使直线与x轴平行,直线与直线y=x﹣2交于点M,与双曲线y=![]() (k≠0)交于点N,若点M在N右边,求n的取值范围.
(k≠0)交于点N,若点M在N右边,求n的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
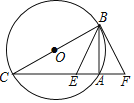
【题目】如图,BC为圆O直径,BF与圆O相切于点B,CF交圆O于A,E为AC上一点,使∠EBA=∠FBA,若EF=6,tan∠F=![]() ,则CE的长为_____.
,则CE的长为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
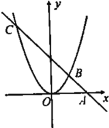
【题目】如图,直线y=kx+b过x轴上的点A(2,0),且与抛物线![]() 交于B,C两点,点B坐标为(1,1).
交于B,C两点,点B坐标为(1,1).
(1)求直线与抛物线对应的函数表达式;
(2)当![]() 时,请根据图象写出自变量x的取值范围;
时,请根据图象写出自变量x的取值范围;
(3)抛物线上是否存在一点D,使![]() ?若存在,求出D点坐标;若不存在,请说明理由
?若存在,求出D点坐标;若不存在,请说明理由
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com